Question

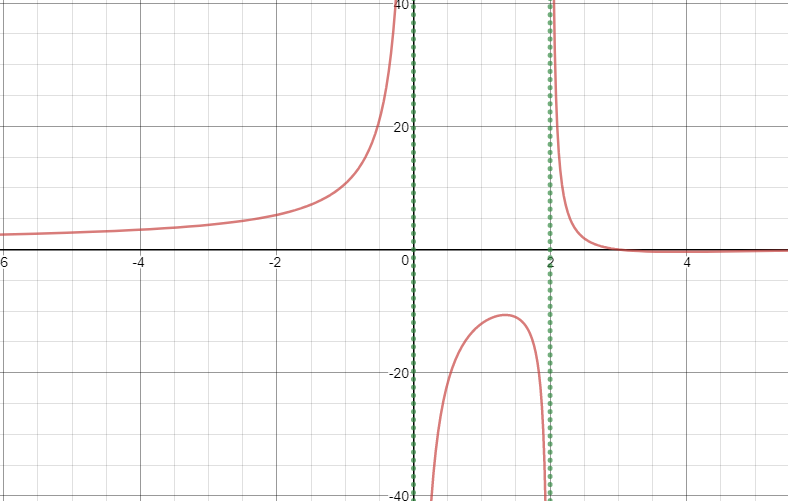
What are the asymptotes and removable discontinuities, if any, of `f(x)= ((x-3)(x-7))/(x(x-2)`?

Answer 1

Asymptotes: `x=0, -2`
Removable Discontinuities: None

Explanation:

Given a function that is already factored makes this process much easier:

To determine asympototes, factor the denominator as much as you can. In your case, it already is factored.

Vertical Asymptotes occur when the denominator equals zero, and since there are multiple terms in the denominator, there will be an asymptote whenever any of the terms is equal to zero, because anything times zero is still zero.

So, set one of your factors equal to zero and solve for `x`, and what you get will the the value of `x` where there is an asymptote. Repeat this for all the factors in the denominator.

Removable Discontinuities occur when there is the same factor in the numerator and denominator. In you case, all the factors are different so there are no Removable Discontinuities.

Desmos Graph for reference: