Question

What is the horizontal range of the stone when the stone strikes the ground?

A person is standing on top of a hill that slopes downwards uniformly at an angle ! with respect to the horizontal. The person throws a stone at an initial angle !0 from the horizontal with an initial speed of v0 . You may neglect air resistance. What is the horizontal range of the stone when the stone strikes the ground?

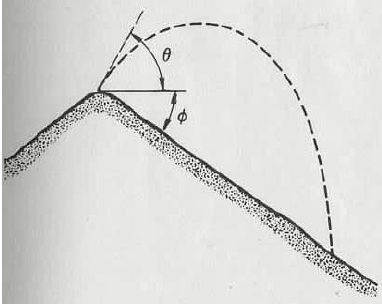
Can I set the coordinate system as follows: Choose the origin to be at the tip of the inclined plane, the x-axis along the inclined plane and the y-axis perpendicular to the inclined plane.
With this coordinate system, the angle the initial speed makes with the x-axis is θ+Φ. We resolve the acceleration due to gravity and initial velocity vector into their 2 components
ax+ay=(gsinΦ)i-(gcosΦ)j
v0=vxi+Vyj=v0cos(θ+Φ)i+v0sin(θ+Φ)j
Then write down the complete set of kinematics for each independent direction x and y describing the position and velocity at instant, t.
Why is my approach to solving the problem incorrect?

Answer 1

I can answer in principle, but not give a specific answer as the data hasn't appeared in the question.

Explanation:

Firstly, make sure you analyse vertical and horizontal motion separately - they are completely independent.

You need to find the time of flight (suggest `s = ut + 1/2at^2`) just looking at the trajectory in the vertical plane and then, as there is no air resistance, realise that the horizontal velocity is constant, so just use `v = s/t` to find the horizontal displacement.

Answer 2

Yes, you could set the coordinate system as you suggest; and then convert from down the slope distance to horizontal distance for the final answer.

Explanation:

If you did what you suggested, and it was marked incorrect, I suspect you did not then convert down the slope distance to horizontal distance. If the distance down the slope you calculated was x, then the horizontal range, `s_h` would be
`s_h = x*cosphi`

I hope this helps,
Steve

Answer 3

See below.

Explanation:

Assuming the origin of coordinates at the very top, the kinematic movement equations are

`(x,y) = (v_0 costheta t, v_0 sin theta t -1/2g t^2)`

The inclined plane is described by

`(x,y) = d (cos phi, -sin phi)`

so the intersection is given at

`{((v_0 cos theta) t = d cos phi), ((v_0 sin theta) t - 1/2g t^2 = -d sin phi):}`

now solving for `t,d` we obtain

#{(t =(2 sin(theta+phi)v_0)/(cosphi g)), (d = ( 2 costheta sin(theta+phi) v_0^2)/(cos^2phi g)):}#