Question

The vertex of the right angled triangle lies on the straight line `2x-y-10 = 0` and the two other vertices, at points `(2,-3)` and `(4,1)` then the area of the triangle is?

A)`sqrt10`
B)`3`
C)`33/5`
D)`11`

Answer 1

This is a higher level question which implies you are at a higher level of ability. So I will let `ul("you")` check that I am correct and finish off the calculations.

Explanation:

`color(blue)("Initial investigation")`
`color(red)("The axis scales are not the same so the graph is distorted")`

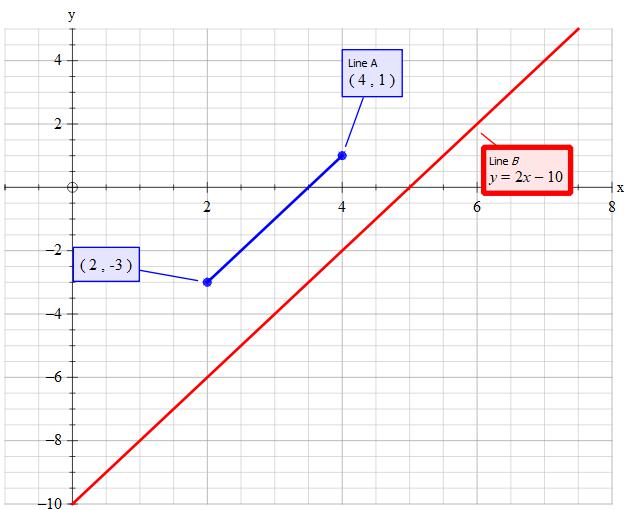
It does not matter where on line B the other vertex is. The area of a triangle is `ul("always")` vertical height times half the base

So we need to determine the equation of the line that is 'vertical' to line A. Make that line pass through its point (4,1) and determine its intersection with line B. From that find the distance between the relevant points and we have got it!

Line A and B have the gradient of 2. So the gradient of the line vertical to them is `-1/2`

This its equation is `y=-1/2x+c`

It passes through the point `(x,y)->(4,1)` giving

`1=-1/2(4)+c-> c=1+2=3`

`color(brown)("Now we determine the shared point")`

Thus we have:

`y=-1/2x+3" "....Equation(1)`
`y=+2x-10" "...Equation(2)`

Consider `Equation(1)`

`x=-2(y-3)`

`x=-2y+6" "......Equation(1_a)`

Substitute `Eqn(1_a)" into "Eqn(2)`

`y=2(-2y+6)-10`

`y=-4y+2`

`5y=2`

`y=2/5`

Substitute back into `Eqn(2)` to find `x`

`y=2x-10color(white)("d")->color(white)("d")2/5=2x-10`

`color(white)("ddddddddddd")->color(white)("d")x=1/5+5= 26/5`

So the vertical height is the distance between

`( 4,1) and (26/5,2/5)`

So `"Area"=1/2"base" xx "height is"`

`=1/2sqrt((4-2)^2+(1+3)^2)xxsqrt( (26/5-4)^2+(2/5-1)^2)`

`=1/2xxsqrt20xx3/sqrt5=1/2xx2sqrt5xx3/sqrt5=3` squnit

`color(red)(" So option B is correct")`

.

Answer 2

I got the option (B) i.e 3squnit

Explanation:

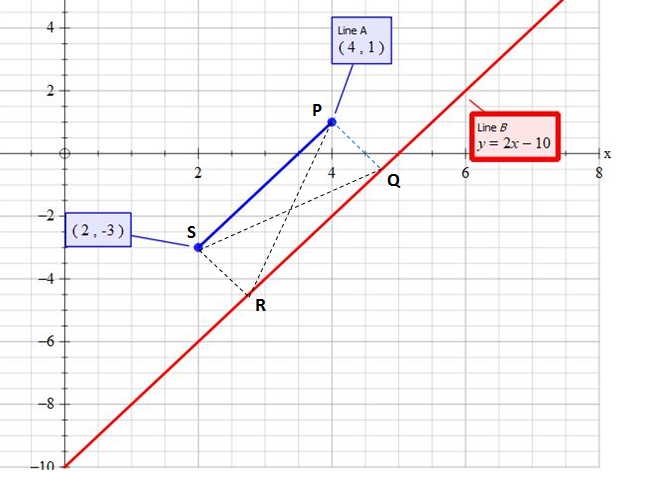
The equation of the given line is `2x-y-10=0 or y-2x+10=0` the slope of this straight line is `2`. The vertex of the right angled triangle is on this line.

Again the line segment joining two points `(2.-3)` and `(4.1)` forms the base of the triangle .

The slope of the line segment forming base is `(1-(-3))/(4-2)=2`. This slope being same as the slope of the given straight line we can say that the base of the triangle is parallel to the given st line on which the vertex of the triangle lies.

Hence we can also say that the length of the perpendicular from any of the two given points on the given straight line on which the vertex of the triangle lies, will represent the height of the required triangle .

Applying the formula of length of the perpendicular from a point `(x_1,y_1)` to the straight line `ax+by+c=0` ( this equation to be written in the form where the sign of c is kept positive)

Length of the perpendicular `(ax_1+by_1+c)/sqrt(a^2+b^2)`

So height of the triangle which is the length of the perpendicular from `(4,1)` to `y-2x+10=0`

`h=(1-2xx4+10)/sqrt(2^2+1^2)=3/sqrt5`

The length of the base of the triangle

`B=sqrt((1+3)^2+(4-2)^2)=sqrt20=2sqrt5`

Hence the area of the triangle `Delta=1/2xxBxxh`

`+1/2xx2sqrt5xx3/sqrt5=3` squnit

The two possible triangles are

`DeltaS PR`

`Delta SPQ`