The circle c has the centre at (3,2) and passes through the point (2,1) determine whether the point with coordinates(4,7) lies on or in the circle ?

Question

2104 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-10-15T10:26:07

the point #(4;7)# is external to the circle

Let's find the radius by calculating the distance between the center and the given point belonging to the circle:

#r=sqrt((x_P-x_C)^2+(y_P-y_C)^2)#

Let #P=(2;1)# and #C=(3;2)#

Then #r=sqrt((2-3)^2+(1-2)^2)=sqrt2#

The distance between the center C and the point #(4;7)# is

#d=sqrt((4-3)^2+(7-2)^2)=sqrt26#
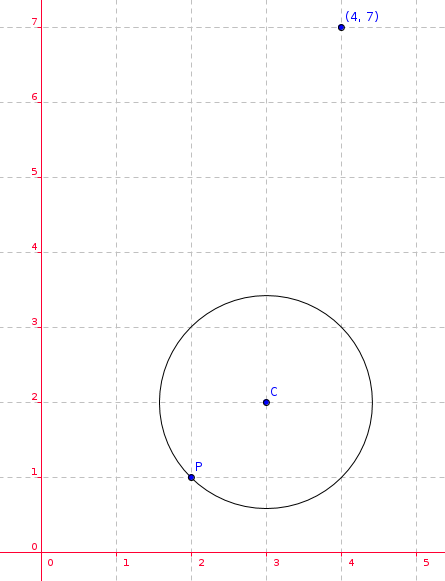
enter image source here

Since #d>r# we conclude that the point #(4;7)# is external to the circle