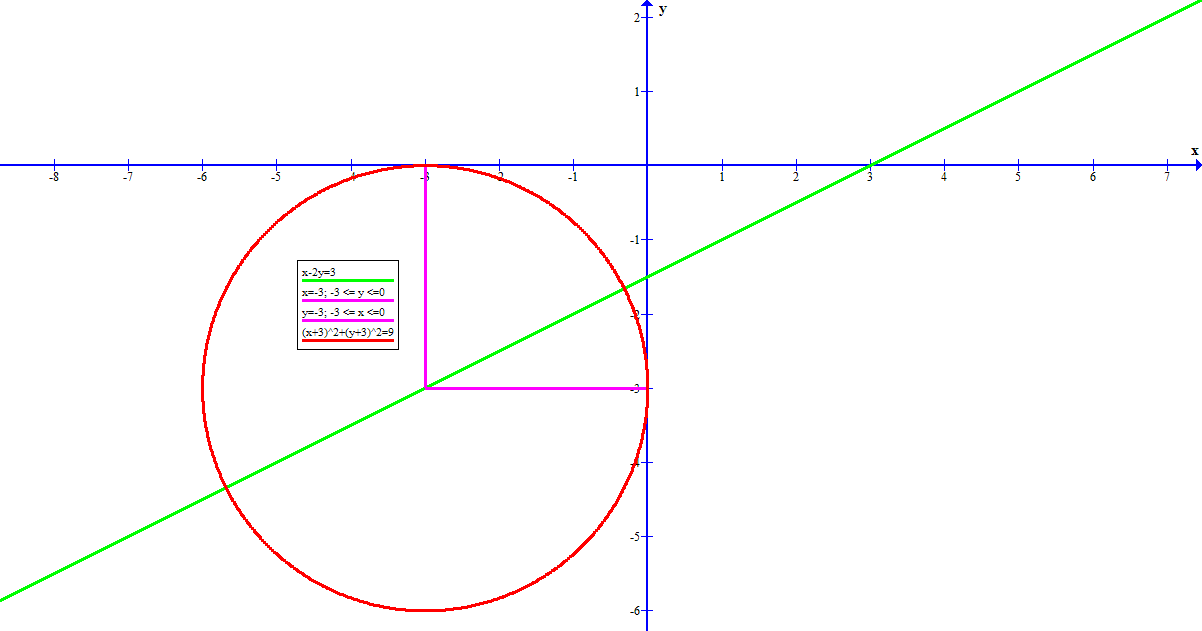
Find the equation of circle which touches both the negative axes and has its center on the line x-2y=3.?
1 Answer
Oct 23, 2017
Explanation:
The center of the circle must have equal
For the line
this means that (after substituting
and similarly
With a center at
the equation of the circle is
or