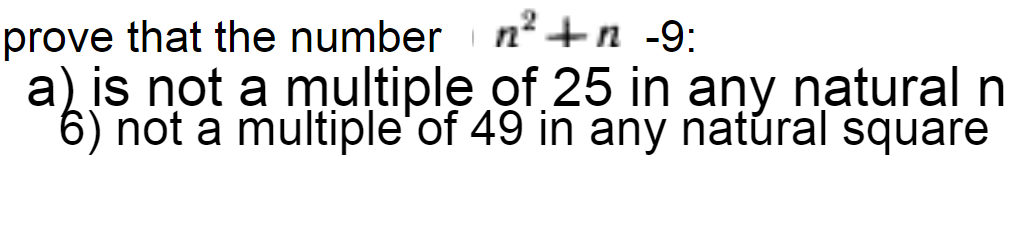(a) #25=5^2#. If the number is not divisible by 5, it is not also divisible by 25.
Let's see if #n^2+n-9# is divisible by 5 or not.
For example, if #n# is divisible by 5, there is an integer #k# that satisfies #n=5k#.
Substitute #n=5k# into #n^2+n-9#:
#n^2+n-9=(5k)^2+(5k)-9#
#=25k^2+5k-9#
#=5(5k^2+k-2)+1#.
Thus, the remainder is 1. #n^2+n-9# is not divisible by 5 if #n=5k#.
We can express this in congruence.
If #n≡0# (mod #5#) then #n^2+n-9≡0+0-9≡-9≡1# (mod #5#)
For other cases(#n≡1,2,3,4# (mod #5#)), see the table.
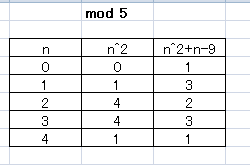
#n^2+n-9# is not a multiple of #5# in any cases, neither is it a multiple of #25#.
(b) #49=7^2#.
Similarly to (a), find the remainder (mod #7#) first.
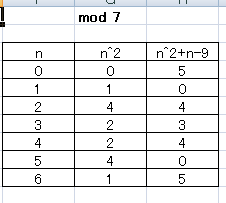
If #n≡0,2,3,4,6# (mod #7#), #n^2+n-9# is a not divisible by #7# and it is proven that #n^2+n-9# is not a multiple of #49#.
If #n≡1# or #n≡5# (mod #7#), #n^2+n-9# is a multiple of #7#.
Now let's move to the next stage.
How to show that no natural square #n=m^2# satisfies (A),(B)?
(A) #n≡1,5# (mod #7#)
(B) #n^2+n-9≡0# (mod #49#)
Since #m^2≡0,1,2,4# (mod #7#), we can confine to the case #n=m^2≡1# (mod #7#). In this case, #m# must satisfy #m≡1,6# (mod #7#) , i.e. #m≡1,6,8,13,15,20,22,27,29,34,36,41,43,48# (mod #49#).
Here is a table for #m, n=m^2, n^2=m^4 and n^2+n-9=m^4+m^2-9#.
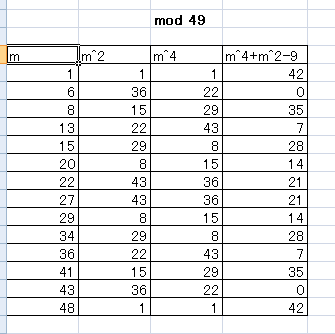
Oops! #n^2+n-9=m^4+m^2-9# is divisible by #49# if #m≡6,43# (mod #49#) and the statement is false.
For example:
#m=6, n=6^2=36#
#n^2+n-9=36^2+36-9=1323=49*27#.