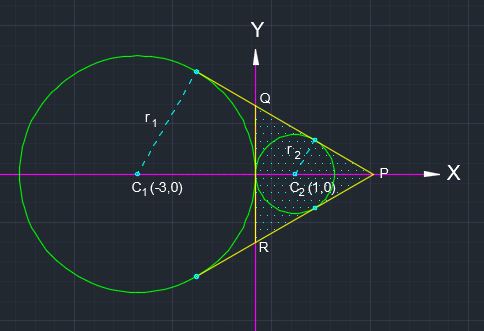
Circle 1 : #x^2+y^2+6x=0, =># center #C_1=(-3,0) , r_1=3#,
Circle 2: #x^2+y^2-2x=0, =># center #C_2=(1,0), r_2=1#
As the two circles touch each other externally, they have 3 common tangents.
Obviously, Y-axis #(x=0)# is one of the common tangents.
Let #y=mx+c# be the equation of the other tangents.
Circle 1 : # x^2+(mx+c)^2+6x=0#
#=> x^2+m^2x^2+2mcx+c^2+6x=0#
#=> (1+m^2)x^2+2(mc+3)x+c^2=0#
As the line #y=mx+c# is tangent to the circle, it touches the circle at one point, so set the discriminant #b^2-4ac# equal to #0#,
#=> (2(mc+3))^2-4(1+m^2)c^2=0#
#=> 4(mc+3)^2-4(1+m^2)c^2=0#
#=> (mc+3)^2-(1+m^2)c^2=0#
#=> m^2c^2+6mc+9-c^2-m^2c^2=0#
#=> 6mc=c^2-9# ----------- #color(red)(EQ(1))#
Similarly, Circle 2 : #x^2+(mx+c)^2-2x=0#
#=> (1+m^2)x^2+2(mc-1)x+c^2=0#
similarly, set the discriminant #b^2-4ac=0#,
#=> 2mc=-c^2+1# ------------#color(red)(EQ(2))#
Solving #EQ(1) and EQ(2)# gives #c=+-sqrt3#
a) when #c=sqrt3, => m=-1/sqrt3#
b) when #c=-sqrt3, => m=1/sqrt3#
#=># equations of the two tangents :
#y=-1/sqrt3x+sqrt3, => sqrt3y=-x+3#, and,
#y=1/sqrt3x-sqrt3, => sqrt3y=x-3#
Setting #x=0, sqrt3y=-x+3, and sqrt3y=x-3# equal to one another, we get :
#P=(3,0), Q=(0,sqrt3) and R=(0,-sqrt3)#
As #PQ=PR=QR=sqrt12=2sqrt3#,
#=> DeltaPQR# is an equilateral triangle.
#=># area of #DeltaPQR=sqrt3/4*(2sqrt3)^2=3sqrt3 " units"^2#
