A pyramid has a parallelogram shaped base and a peak directly above its center. Its base's sides have lengths of 2 and 8 and the pyramid's height is 2 . If one of the base's corners has an angle of (5pi)/6, what is the pyramid's surface area?
2 Answers
Total Surface Area # T S A = 34.8328
Explanation:
Area of parallelogram base
Area of
Area of
Lateral surface area =
Total surface area =Area of parallelogram base + Lateral surface area
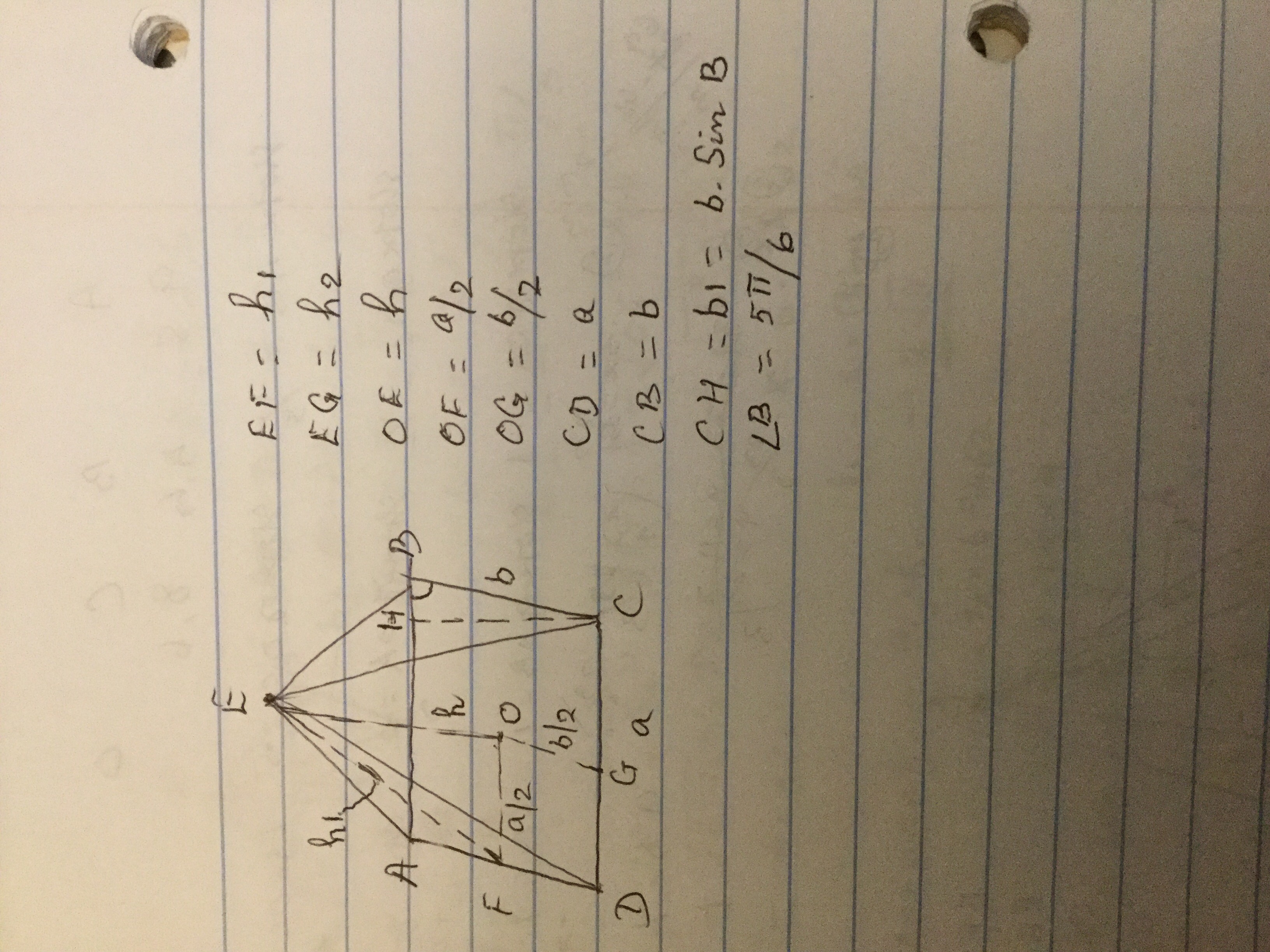 Total Surface Area T S A = **14.4755**enter image source here
Total Surface Area T S A = **14.4755**enter image source here
The pyramid's surface area is
Explanation:
I recommend to use coordinates to solve this problem.
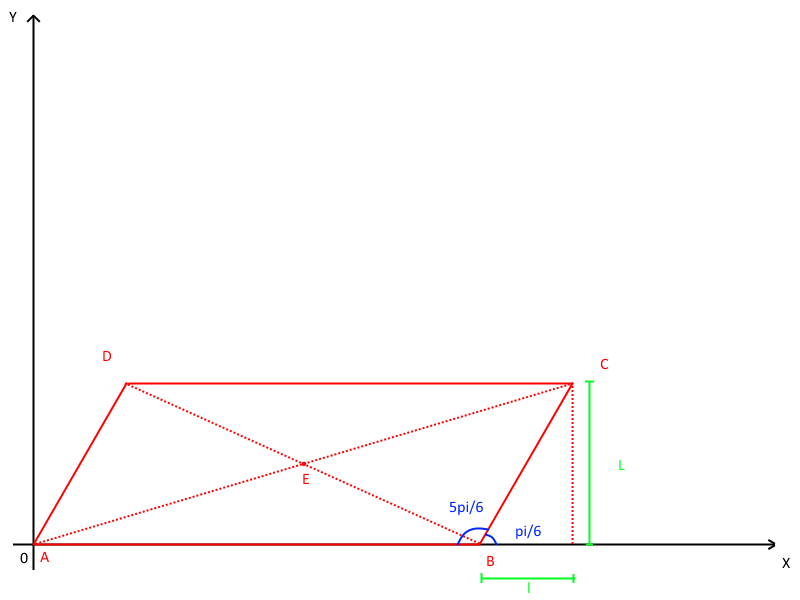
The pyramid's base is ABCD and its center is E
The coordinates of A and B are:
In order to find the coordinates of C and D, we need to use trigonometry and the pythagorean theorem:
Therefore the coordinates of C and D are:
A parallelogram's diagonals cross mid-length, thus the coordinates of E are:
If the base is located in the (x;y) plane and the pyramid's peak (called F) is located at 2 above E, then the coordinates of all the pyramid's points are:
The pyramid's base's surface area is
The ADF and BCF sides' surface areas are:
The ABF and CDF sides' surface areas are:
Therefore, the pyramid's total surface area is:
