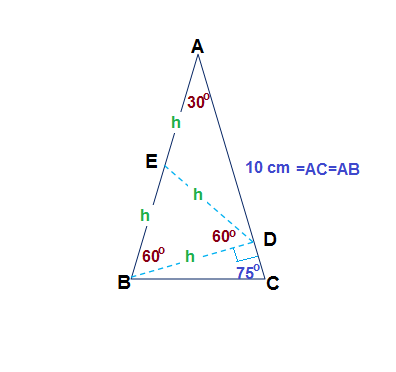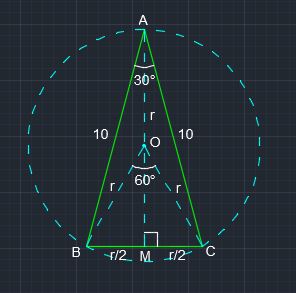
Let #O# be the center of the circumcircle of #DeltaABC#,
let #r# be the circumradius, #=> OA=OB=OC=r#,
given #angleBAC=30^@, => angleBOC=2xx30=60^@#
#=> DeltaOBC# is an equilateral triangle
#=> OB=OC=BC=r#
#color(red)(i))# consider #DeltaOBM#,
#OM^2=r^2-(r/2)^2=3/4r^2, => OM=sqrt3/2r#
consider #DeltaABM#,
#10^2=(r+sqrt3/2r)^2+(r/2)^2#
#=> 100=(1+sqrt3+3/4+1/4)r^2=(2+sqrt3)r^2#
#=> r^2=(100)/(2+sqrt3)#
#=># area of #DeltaABC=1/2*BC*AM#
#= 1/2*BC*(AO+OM)#
#=1/2*r*(r+sqrt3/2r)#
#=1/2*r^2(1+sqrt3/2)#
#=1/2*(100)/(2+sqrt3)*(2+sqrt3)/2=25 " unit"^2#
#color(red)(ii))# we can also use the following formula to find the area of #DeltaABC# :
recall that area of a triangle with sides #a,b and c#, and its circumradius #=r# is given by : #A'=(abc)/(4r)#
Here, as #AB=AC=10, and BC=r#,
#=># area of #DeltaABC=(10xx10xxr)/(4r)=100/4=25 " unit"^2#