Question #0994c
1 Answer
Explanation:
Orient the triangle so that BC, is on the x axis, point B is
The coordinates of point
Here is a graph of what I have described thus far:
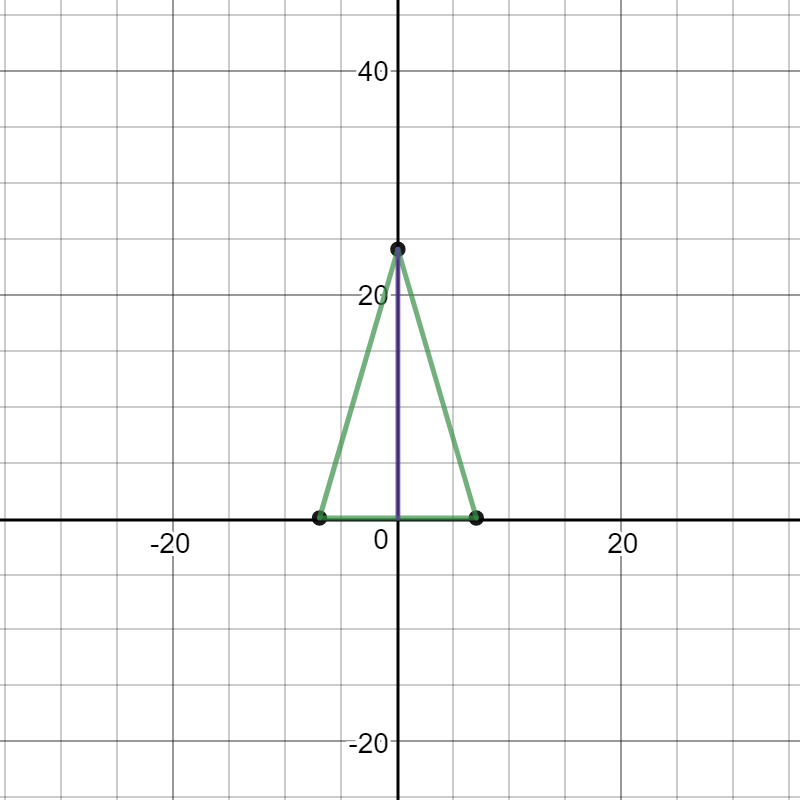
Please observe that, the points A, B, and C are in black, the sides of
The slope of the line AC is the slope from point
The slope, n, of its perpendicular bisector is:
The perpendicular bisector will go through the midpoint between A and C:
The point-slope form of the equation of the perpendicular bisector is:
Here is a graph of the triangle with the perpendicular bisector:
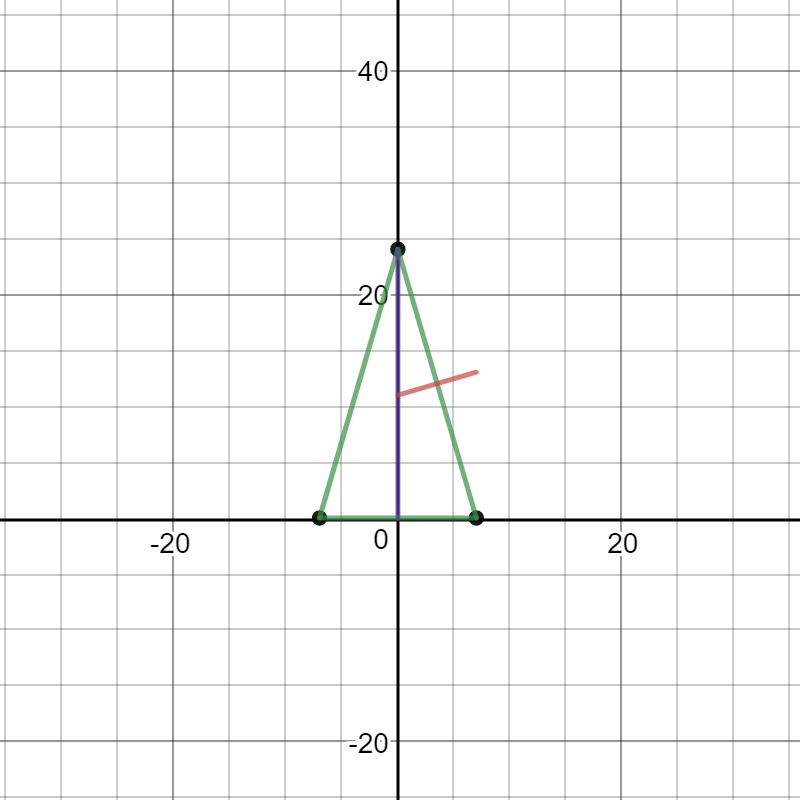
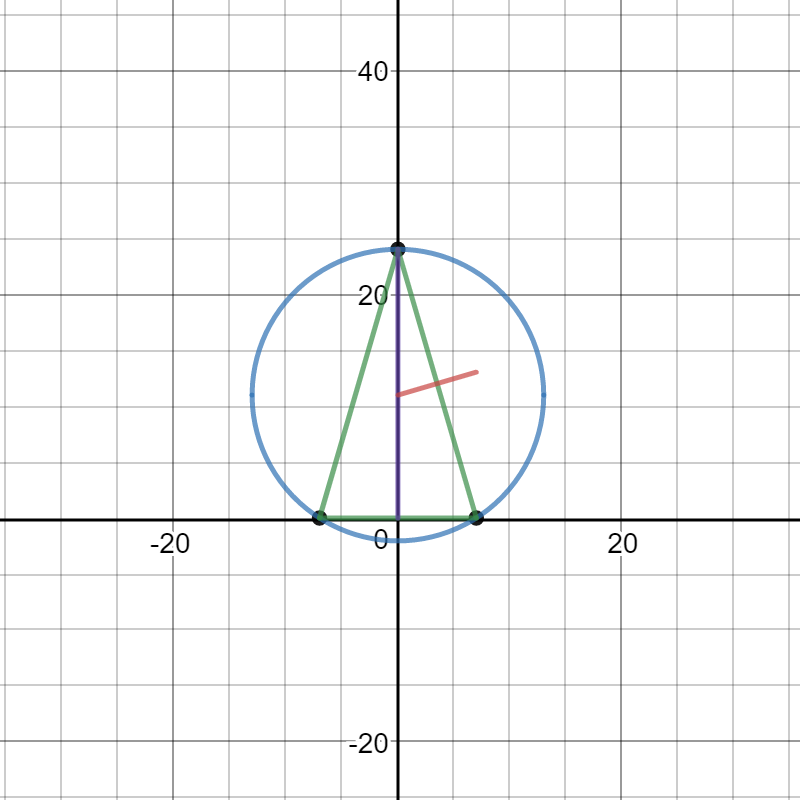
The center of the circle is the point where this line intercepts the y axis:
The radius of the circle is the distance from the y intercept to point A
Here is a graph with the circle added.