Question #d43f9
1 Answer
Explanation:
Start by recalling what the general Taylor series polynomial is. The purpose is to find an approximation of the original function centered around some value
The only difference with the Maclaurin series is that
With that formula in hand, we can go about finding the first few derivatives
Next, plug
You can see the pattern that only the odd numbered derivatives have a non-zero solution. Finally, stick them in in the Maclaurin formula above
Removing the zeros and simplifying the factorials gives
You can see that even these three terms (in red) follows the original function (in blue) for some distance.
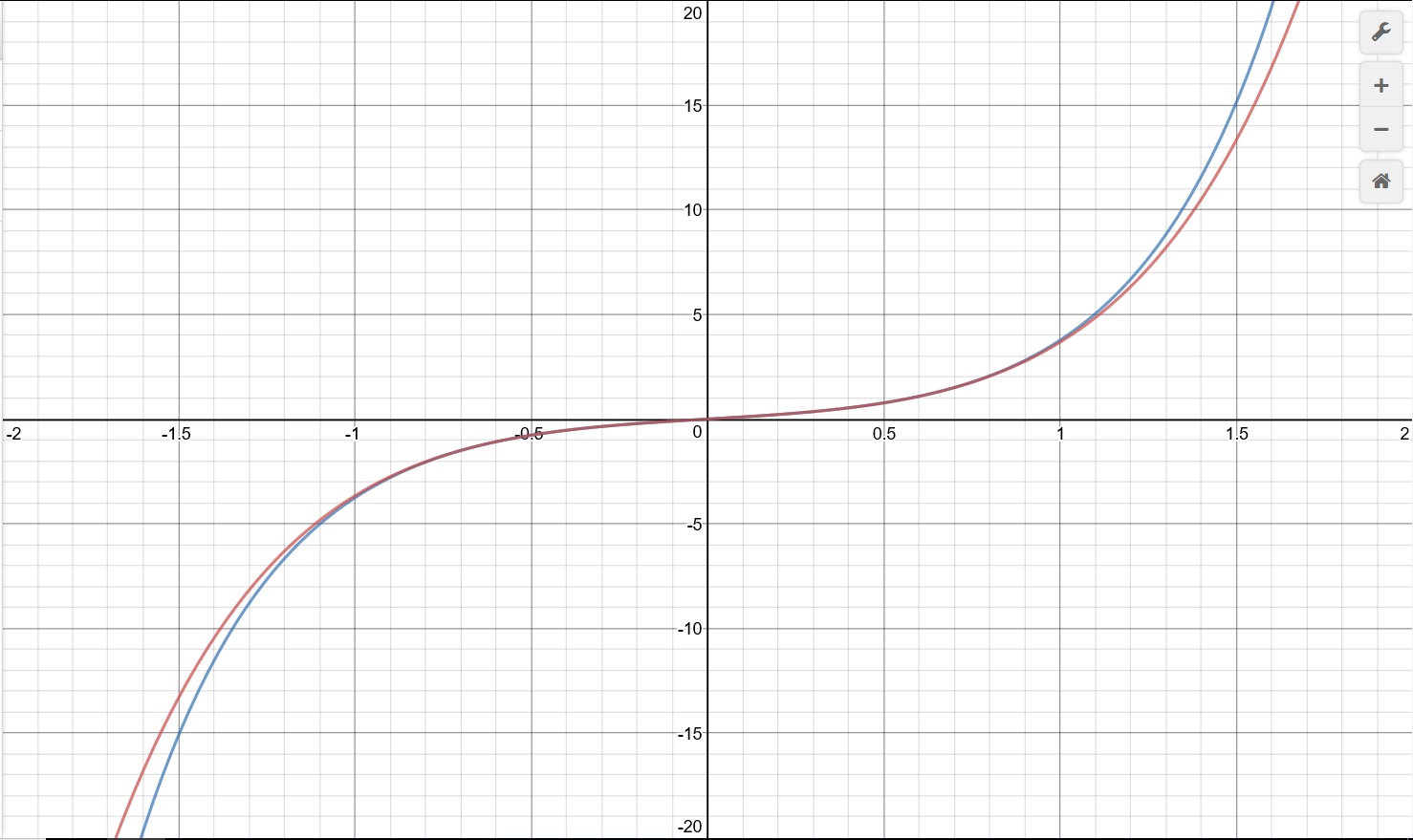
I had to expand the window to
