Question

How do you find the angle in radians between the vectors a = <sqrt(3), -1> and b = <0, 3>?

We haven't gone over this and I'm lost on the homework. Please provide lots of steps so that I can follow along and learn to do other problems like this by myself! Thank you!

Answer 1

See below.

Explanation:

`A=((sqrt(3)),(-1))`

`B=((0),(3))`

In order to find the angle between two vectors, we use the Dot Product. This is also sometimes referred to as the Inner Product or the Scaler Product.

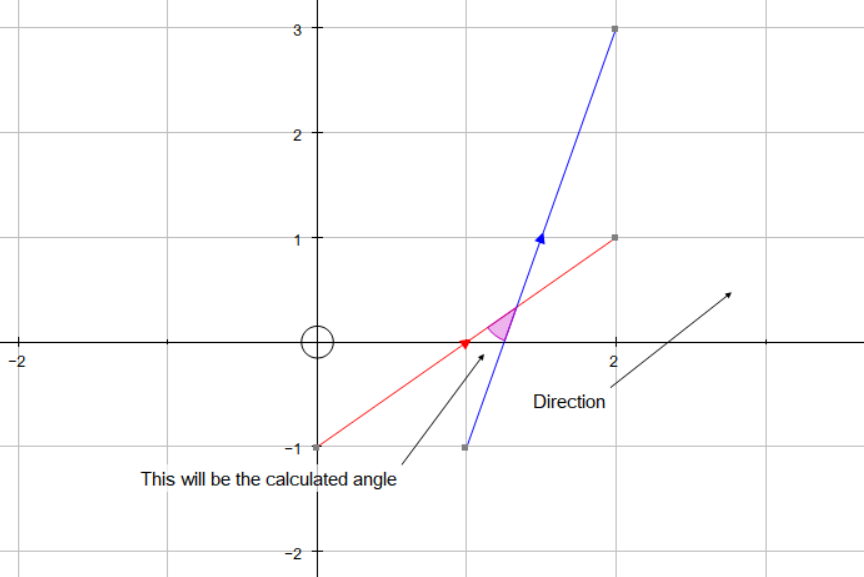
The angle we calculate, will be the angle between the two vectors where they are heading in the same relative direction. See diagram.

The Dot Product is defined as:

`A*B = ||A||*||B||*cos(theta)`

The product of the vectors is defined as follows:

`A*B=((sqrt(3)),(-1))*((0),(3))=sqrt(3)xx0+(-1)xx3=-3`

This is the product and sum of corresponding components and is different to how we normally multiply brackets in algebra.

Magnitude is found using Pythagoras' theorem, so:

`||A||= sqrt((sqrt(3))^2+(-1)^2)=sqrt(4)=2`

`||B||= sqrt((0)^2+(3)^2)=sqrt(9)=3`

We are only interested in positive roots here, as magnitude is an absolute value.

So far we have:

`A*B = ||A||*||B||*cos(theta)`

`-3 = 2xx3xxcostheta`

`-3 = 6xxcostheta`

`-3/6 =costheta`

`costheta=-3/6=-1/2`

We now find the angle that corresponds to a cosine of `-1/2`

`theta=cos^-1(costheta)=cos^-1(-1/2)=pi-pi/3=color(blue)((2pi)/3)`

So `color(blue)((2pi)/3)` is the required angle.

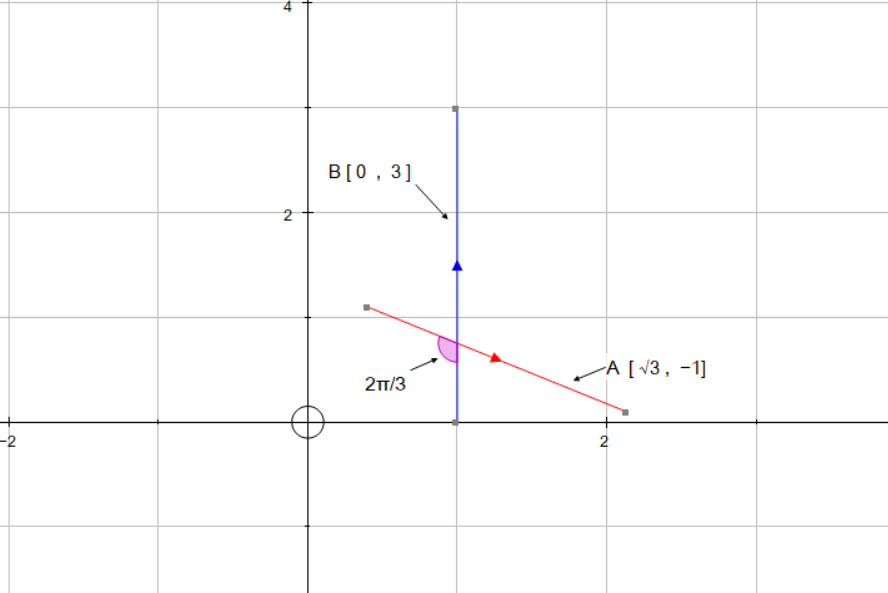
I hope this helps you.