Find a formula for the inverse function?
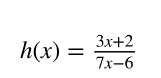
I think that you multiply a number on each side but I'm really confused on how to find the inverse?
I think that you multiply a number on each side but I'm really confused on how to find the inverse?
2 Answers
See explanation.
Explanation:
If you want to find an inverse function of
y=(3x+2)/(7x-6)
first you can multiply both sides by the denominator:
y(7x-6)=3x+2
7xy-6y=3x+2
Now we can rearrange the equation so that the new unknown
7xy-3x=6y+2
x*(7y-3)=6y+2
x=(6y+2)/(7y+3)
Now we can change the variables back. This causes that
The inverse function is:
y=(6x+2)/(7x+3)
Substitute
Explanation:
Given:
Substitute
One of the two parts of the definition of an inverse is that
Multiply both sides by
Distribute the x:
Add 6x to both sides:
Subtract
Factor out
Divide both sides by
To verify that this is truly the inverse, we must test that
Start verification with
Multiply the right side by 1 in the form of
This has the effect of remove the embedded fractions and distributing the denominator over the constants:
Use the distributive property to perform 4 multiplications:
Combine like terms:
Finish the verification with
Multiply by 1 in the form of
Eliminate the embedded fractions and distribute the numerator among the constants:
Use the distributive property to perform 4 multiplications:
Combine like terms:
It is verified that
