A triangle is defined by the three points: a=(7, 10), b=(9, 10), and c= (5, 6). How do I determine all three angles in the triangle (in radians)?

We haven't gone over this yet in class and I'm lost. What equation(s) am I even suppose to use? How would I reason something like this out and know which steps to take?

1 Answer
Somebody N.
Nov 12, 2017

See below.

Explanation:

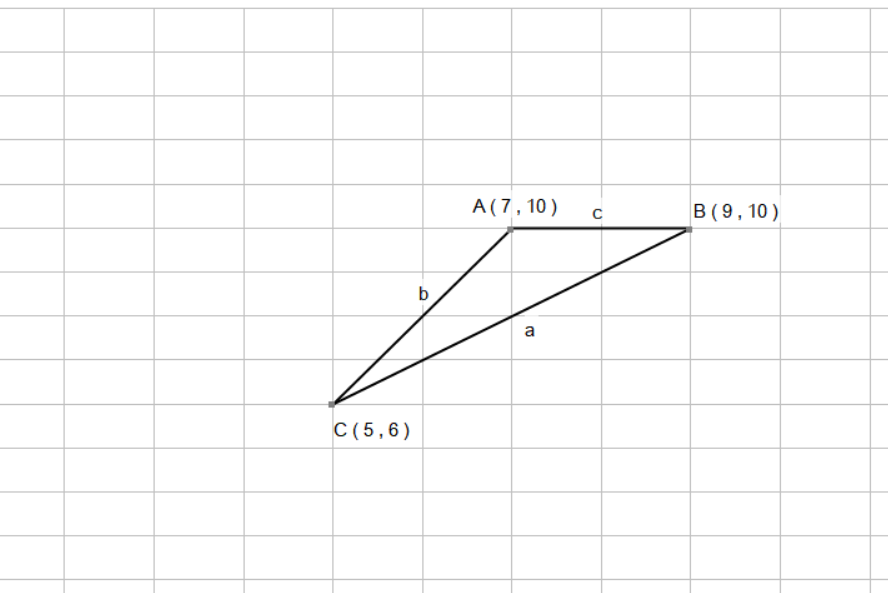
enter image source here

I have marked the triangle in a more conventional way. The first thing we need to do, is find the length of the sides a , b and c. We can do this by using the Distance Formula. The Distance Formula states, where d is the distance, that:

#d= sqrt((x_2-x_1)^2+(y_2-y_1)^2)#

So:

#a= sqrt((9-5)^2+(10-6)^2)=sqrt(32)=color(blue)(4sqrt(2))#

#b=sqrt((7-5)^2+(10-6)^2)=sqrt(20)=color(blue)(2sqrt(5))#

#c=sqrt((9-7)^2+(10-10)^2)=sqrt(4)=color(blue)(2)#

We now know all 3 sides, but since we don't know any angles, we will have to use the Cosine Rule.

The Cosine Rule states that:

#a^2=b^2+c^2-2bc*cos(A)#

Angle A:

#(4sqrt(2))^2=(2sqrt(5))^2+(2)^2-2(2sqrt(5))(2)*cos(A)#

#32=20+4-8sqrt(5)*cos(A)#

#cos(A)=(32-20-4)/(-8sqrt(5))=8/(-8sqrt(5))=-sqrt(5)/5#

#A=cos^-1(cos(A))=cos^-1(-sqrt(5)/5)=color(blue)(2.034)# radians.

We rearrange the formula for angle B.

#b^2=a^2+c^2-2ac*cos(B)#

Angle B:

#(2sqrt(5))^2=(4sqrt(2))^2+(2)^2-2(4sqrt(2))(2)*cos(B)#

#20=32+4-16sqrt(2)*cos(B)#

#cos(B)=(20-32-4)/(-16sqrt(2))=(-16)/(-16sqrt(2))=sqrt(2)/2#

#B= cos^-1(cos(B))=cos^-1(sqrt(2)/2)=pi/4#

Angle C:

#pi-(pi/4+2.034)=0.322#

So solution is:

#a = 4sqrt(2)#

#b=2sqrt(5)#

#c=2#

#A=2.034# radians.

#B=pi/4# radians

#C= 0.322# radians

3 .d.p.

Related questions
Impact of this question
11946 views around the world
You can reuse this answer
Creative Commons License