Question #0e712

Question

Question #0e712

1 Answer

Impact of this question

974 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-11-15T19:37:26

$A_{Total} = 8 \sqrt{2} \approx 11.31$ $A_"Total"=8sqrt(2)~~11.31$

Explanation:

Although this question is marked as a Trigonometry question, the solution requires calculus to solve.

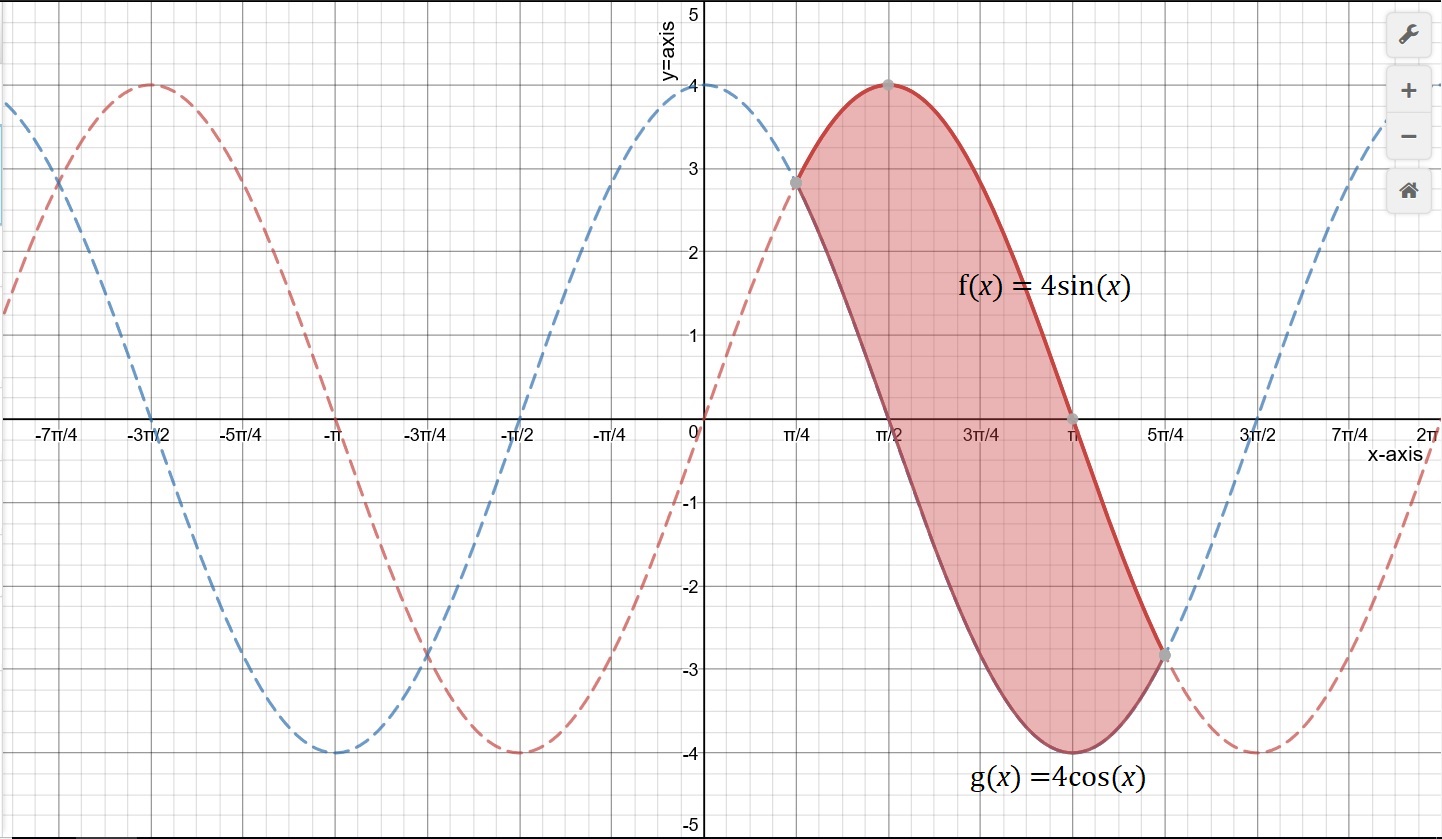
You are given two curves and want to find the space between them, as depicted by this graph.

Let $f (x) = 4 sin (x)$ $f(x) = 4sin(x)$ .

Let $g (x) = 4 cos (x)$ $g(x)=4cos(x)$ .

![Desmos.com and MS Paint]( useruploads.socratic.org )

The $x$ $x$ -coordinate of the left hand side intersection is $a = \frac{π}{4}$ $a=pi/4$ .
The $x$ $x$ -coordinate of the right hand side intersection is $b = \frac{5 π}{4}$ $b=(5pi)/4$ .

The positive area above the $x$ $x$ -axis is equal to the negative area below the $x$ $x$ -axis and would cancel each other out. So we must stick to finding the area above the $x$ $x$ -axis and then double that area.

One strategy would be to find the area, $A$ $A$ under $f (x) = 4 sin (x)$ $f(x)=4sin(x)$ between $x = \frac{π}{4}$ $x=pi/4$ and $x = π$ $x=pi$ and then subtract off the area, $B$ $B$ , of $g (x) = 4 cos (x)$ $g(x)=4cos(x)$ between $x = \frac{π}{4}$ $x=pi/4$ and $x = \frac{π}{2}$ $x=pi/2$ . Finally, we would need to double that area to find the total area, $A_{Total}$ $A_"Total"$ , both above and below the $x$ $x$ -axis. In other words, we are finding $2 (A - B) .$ $2(A-B).$

Area $A$ $A$ is

$A = \int_{\frac{π}{4}}^{π} 4 sin (x) d x = {[- 4 cos (x)]}_{\frac{π}{4}}^{π}$ $A=int_(pi/4)^pi4sin(x)dx=[-4cos(x)]_(pi/4)^pi$
$= 4 + 2 \sqrt{2}$ $= 4+2sqrt(2)$

Area $B$ $B$ is

$B = \int_{\frac{π}{4}}^{\frac{π}{2}} 4 cos (x) d x = {[4 sin (x)]}_{\frac{π}{4}}^{\frac{π}{2}}$ $B=int_(pi/4)^(pi/2)4cos(x)dx=[4sin(x)]_(pi/4)^(pi/2)$

$B = 4 - 2 \sqrt{2}$ $B=4-2sqrt(2)$

Therefore, the total area $A_{Total}$ $A_"Total"$ is

$A_{Total} = 2 (A - B)$ $A_"Total"=2(A-B)$
$= 2 (4 + 2 \sqrt{2} - 4 + 2 \sqrt{2})$ $" "=2(4+2sqrt(2)-4+2sqrt(2))$
$= 8 \sqrt{2} \approx 11.31$ $" "=8sqrt(2)~~11.31$

Science

Math

Humanities

... and beyond

Question #0e712

1 Answer

Explanation:

Related questions

Impact of this question