Solve for #x# in #|2x-4| >= -5#? Why doesn't the usual method work in this case?
At first I was blindly solving and got #-0.5<=x<=4.5# . However, the answer is obviously all reals because the absolute value of anything will be positive; therefore, #abs(2x-4)# must be greater than #-5# .
Why doesn't the usual method work in this case?
At first I was blindly solving and got
Why doesn't the usual method work in this case?
1 Answer
Since all modulus values are bigger or equal to
Square both sides which gets rid of the modulus function,
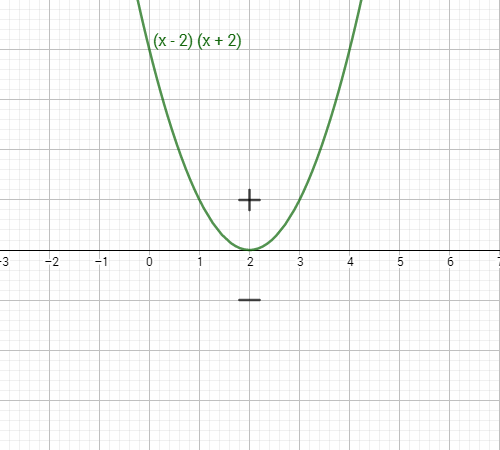
Hence, the solution is all real roots.
All absolute values must be equal or bigger to
So, why doesn't the usual method work?
That is because we normally do this:
Square both sides which gets rid of the modulus function,
This is because we squared a negative number to make it positive, where in fact, is impossible as all absolute values are positive. Hence, the equation automatically implies that

