Question

A rhombus has sides `8 cm` in length and its shortest diagonal is `10 cm` in length. What is the area of the rhombus to the nearest `cm^2`?

Answer 1

Refer to explanation

Explanation:

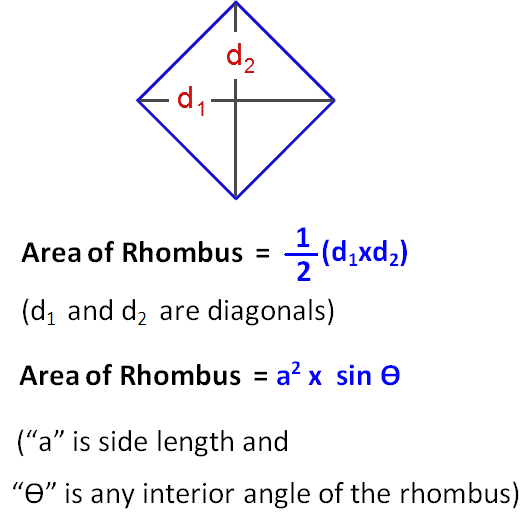
As you can see from the diagram, the area of a rhombus is the the two diagonals multiplied together and divided by 2.

From the information given in the problem, we know the each side of the rhombus is `8cm` and the shortest diagonal( the vertical diagonal I presume) is `10cm`. We have to work out what is the length of the horizontal diagonal before working out the area.

We are first going to cut in fours,as shown in the diagram, having the hypotenuse as 8cm and the opposite as 5cm. To find the adjacent, we will use Pythagora's theorem.

`a^2+b^2=c^2`

We want the adjacent so rearrange the equation to make `a^2` the subject.

`a^2= c^2-b^2`

To remove the square, take the square root of the equation.

`a = sqrt(c^2-b^2)`

Now substitute the values for b and c to calculate a.

`a= sqrt(8^2-5^2)`
`a= sqrt(39)` (Keeping the surd for the sake of no rounding mistakes)

Since it is half the length, multiply `sqrt39` by `2`

`sqrt39 * 2 = 2sqrt39`

From the diagram, we now know both `d_1` and `d_2`

`d_1 = 2sqrt39cm`
`d_2 = 10cm`

Now apply the formula for the area of a rhombus.

`(10cm * 2sqrt39 cm)/2 = 10sqrt39cm^2 or 62.45cm^2 to 4 s.f`

Answer 2

`"Area" ~~ 62" cm"^2`

Explanation:

The area is the cross product of the two sides.

One definition of the cross product is `vecAxxvecB = |A||B|sin(theta)` where `theta` is the angle between the two vectors.

In the case of a rhombus, the magnitudes are equal to the length of the equal sides and `theta` is the smallest angle between the two sides:

`"Area" = (8" cm")^2sin(theta)" [1]"`

The longest diagonal forms a triangle with the two sides and the largest angle between them, therefore, The Law of Cosines allows us to write:

`(10" cm")^2= (8" cm")^2 + (8" cm")^2 - 2(8" cm")^2cos(pi-theta)`

We know that `cos(pi-theta) = -cos(theta)`:

`(10" cm")^2= (8" cm")^2 + (8" cm")^2 + 2(8" cm")^2cos(theta)`

`(10" cm")^2= 2(8" cm")^2 + 2(8" cm")^2cos(theta)`

`(10" cm")^2= 2(8" cm")^2(1 + cos(theta))`

`100" cm"^2= 128" cm"^2(1+cos(theta))`

`100/128 = 1 + cos(theta)`

`cos(theta) = 100/128-1`

`cos(theta) = -7/32`

`theta = cos^-1(-7/32)" [2]"`

Substitute equation [2] into equation [1]:

`"Area" = (8" cm")^2sin(cos^-1(-7/32))`

`"Area" ~~ 62" cm"^2`