A wave function for hydrogen atom is given below, where #a_0# is the Bohr radius, #"52.9177 pm"#. If the Radial node in 2s be at #r_0#. Then the value of #r_0# in terms of #a_0# is?

Here is the equation:

#ψ_(2s) = color(red)(sqrt(2)/(8pi)) × [1/a_0]^"3/2" [2 - r/a_0]e^(-r//color(red)(a_0))#

  1. #r_0 = 1/2a_0#

  2. #r_0 = 2a_0#

  3. #r_0 = 4a_0#

  4. #r_0 = 2/sqrt(2)a_0#

1 Answer
Truong-Son N.
Nov 20, 2017

#r_0 = 2a_0#

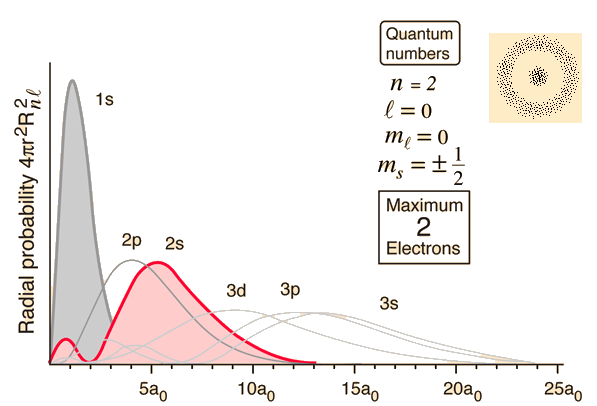
http://hyperphysics.phy-astr.gsu.edu/

First of all, the wave function you have is not correct. The correct wave function is:

#psi_(2s) = color(orange)(1/(4sqrt(2pi))) (1/a_0)^(3//2)(2 - r/a_0)e^(-r//color(orange)(2a_0))#

The radial node occurs where the radial component #R_(nl)(r)# of the wave function goes to zero. But since there is no angular component #Y_(l)^(m_l)(theta,phi)# to a wave function for a spherical orbital (#l = 0, m_l = 0#), set #psi_(2s) = 0#.

All the nonzero constants can be divided out to get:

#0 = |[(2 - r/a_0)e^(-r//2a_0)]|_(r = r_0)#

Since #e^(-r//2a_0) ne 0# for #r# in between #0# and #oo# (where nodes can occur), that can be divided out as well.

#0 = 2 - r_0/a_0#

Therefore, the distance away from the nucleus at which there is a radial node is:

#color(blue)(r_0 = 2a_0)#

or about #2 cdot "52.9177 pm" = "105.8354 pm"#.

Related questions
Impact of this question
6478 views around the world
You can reuse this answer
Creative Commons License