What's the value of h which minimize the perimeter?
Consider a window the shape of which is a rectangle of height h surmounted by a triangle having a height T that is 0.9 times the width w of the rectangle (as shown in the figure below).
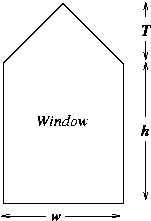
If the cross-sectional area is A , determine the dimensions of the window which minimize the perimeter.
I found the value of w but couldn't find the value of h .
Consider a window the shape of which is a rectangle of height

If the cross-sectional area is
I found the value of
1 Answer
See below.
Explanation:
Cross sectional area
Perimeter
so calling
we have
find
subjected to
substituting
and
giving
and consequently

