How do you prove #a=v^2/r# and #a=r\omega^2# using a circle and vector diagram?

Question

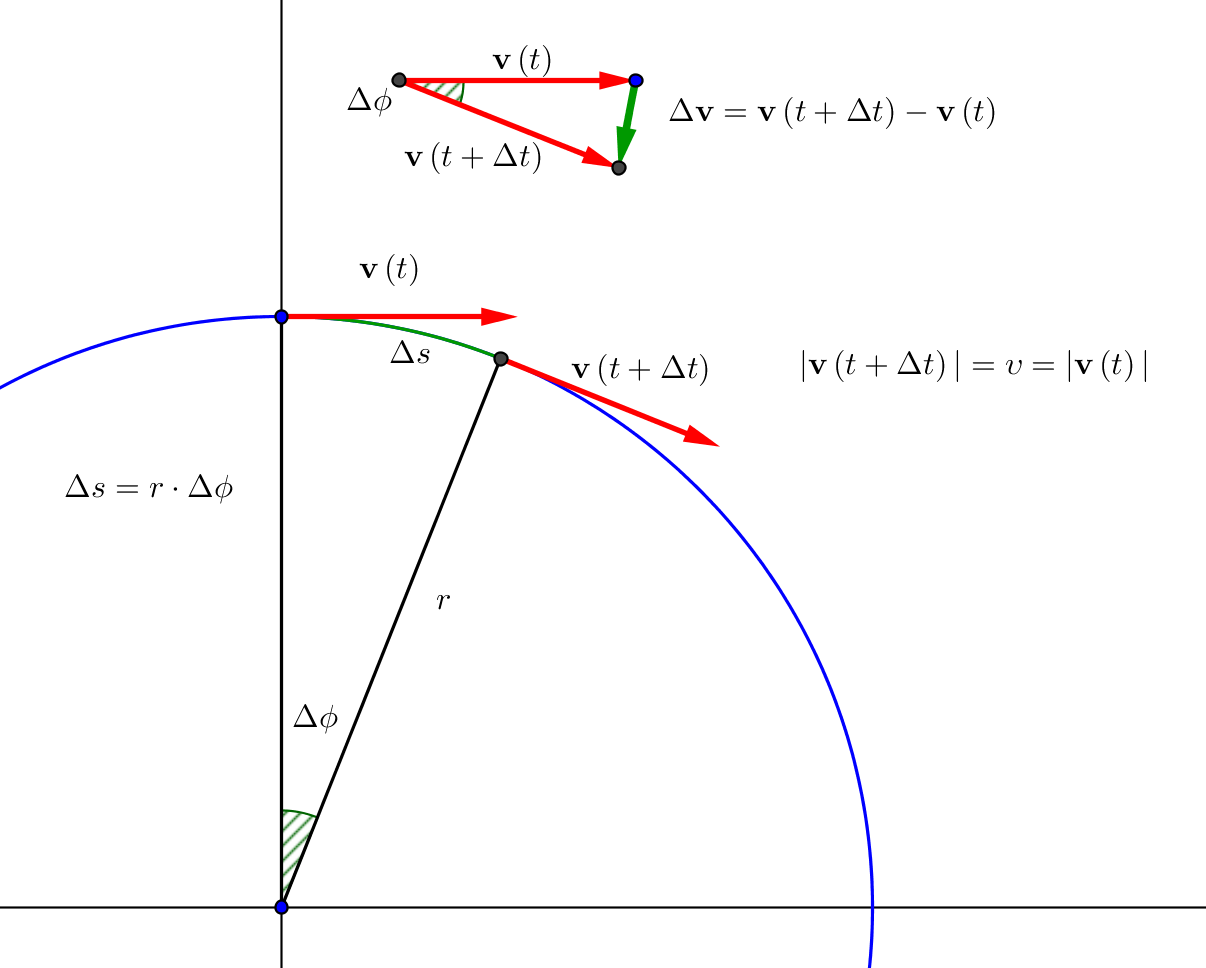
I know you start off with a circle and two points on the circumference. Each point has an arrow tangent to the circle and are facing the same way (in terms of rotation).

Then, you connect the two points to the center, and label each line #r#, and the angle between them #\theta#.

The vector diagram has the two arrows connected tail to tail, with an angle of #\theta#. An arrow is drawn from head to head, and is the force provided (#abs(v_1)+abs(v_2)#). It also has something to do with #sin\theta=\theta# for very small angles or something similar.

I'm not sure where to go from there.

Please do not use derivative, and other vector stuff. Also include diagrams.

26726 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-11-22T13:37:08

See the expplanation below

enter image source here

The acceleration is

#a=(Deltav)/(Deltat)#

#=(vDelta phi)/(Deltat)#

#=(vDeltas)/(rDeltat)#

#=(v.vDeltat)/(rDeltat)#

#=v^2/r#

The angular velocity is

#omega=(Deltaphi)/(Deltat)#

#=(Deltas)/(rDeltat)#

#=(v)/(r)#

#omega^2=(v)^2/(r)^2=(v^2)/(r.r)=a/r#

#a=romega^2#

Addition

#sinDeltaphi=(Deltas)/(r)#

For small angles #sinDeltaphi=Deltaphi#

Dividing by #Deltat#

#sinDeltaphi=Delta phi=(Deltas)/(r)#

#(Deltaphi)/(Deltat)=(Deltas)/(Deltat)*1/r#

#omega=v/r#