Question

Question #5f58b

Answer 1

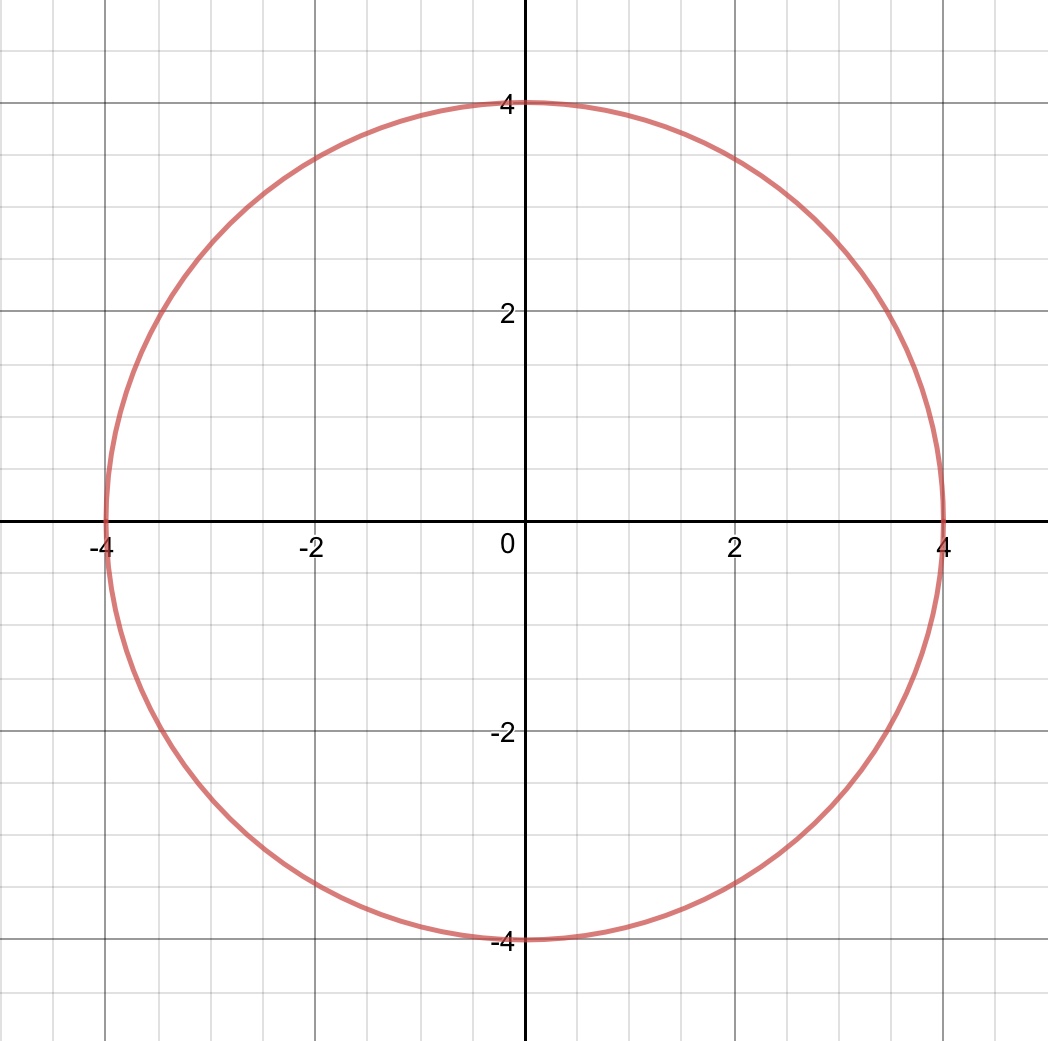
Here's the graph.

Explanation:

Okay, so looking at this equation, we can tell that it is a conic section because `x` and `y` are both squared. Furthermore, we can tell that this is a circle, as it is in the standard form of a circle,

`(x-h)^2+(y-k)^2=r^2`

Where `(h,k)` is the center of the circle and `r` is the radius.

Given that both `h=0` and `k=0`, we know the center is `(0,0)`.

`r^2=16`, which means that our radius is `4`.

The circle has center `(0,0)` and radius `4`.