Question

Question #811ac

Answer 1

`=2sqrt3-(2pi)/3`

Explanation:

.

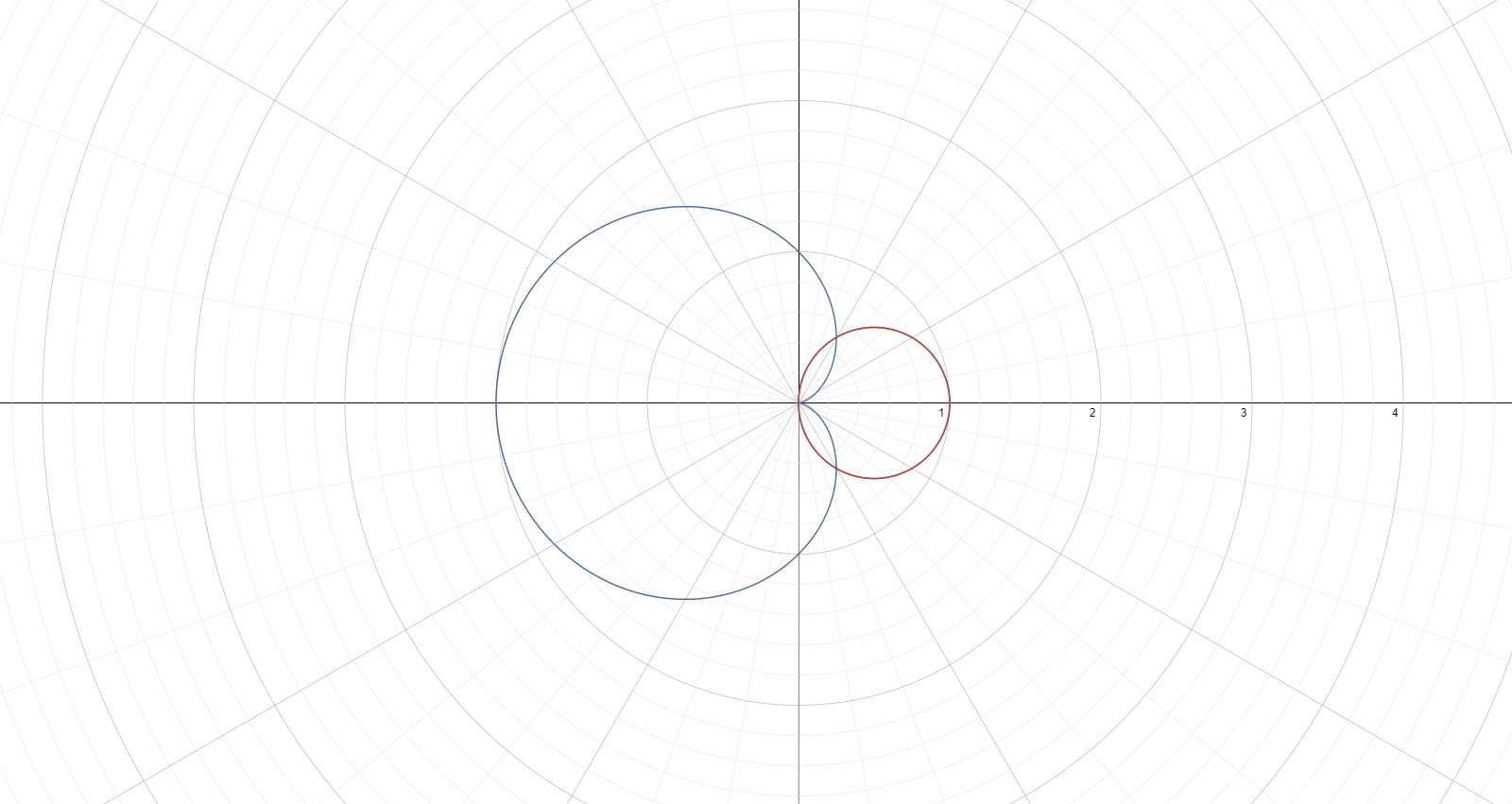
`r=costheta`

`r=1-costheta`

Let's set the two functions equal to each other and solve for `theta` to find the points of intersection:

`costheta=1-costheta`

`2costheta=1`

`costheta=1/2`

`theta=arccos(1/2)=pi/3 and -pi/3`

The enclosed areas are between `0 and pi/3` and between `0 and -pi/3`, and the two are symmetrical. We can figure out the area enclosed between `0 and pi/3` and multiply it by two:

`int_0^(pi/3)(cos^2theta-(1-costheta)^2)(d(theta))`

`int_0^(pi/3)(cos^2theta-(1+cos^2theta-2costheta))(d(theta))`

`int_0^(pi/3)(cos^2theta-1-cos^2theta+2costheta)(d(theta))`

`=int_0^(pi/3)(2costheta-1)(d(theta))=2int_0^(pi/3)costheta(d(theta))-int_0^(pi/3)d(theta)`

`=(2sintheta-theta)_0^(pi/3)=2(sqrt3/2)-pi/3-2sin0-0=sqrt3-pi/3-0-0=sqrt3-pi/3`

Now we multiply it by `2` to get the two enclosed areas together:

`=2sqrt3-(2pi)/3`