Question

Fourier Analysis. `f(x)=x^2 (-1<x<1), p=2` (How about `f(x)`.?)

Answer 1

See below.

Explanation:

`f(x)` is even so

`f(x)= sum_(k=0)^oo a_kcos(k pi x)`

NOTE

`int_-1^1 cos(n pi x) cos(m pi x) dx = 1/pi(Sin((m - n) pi)/(m - n) + Sin((m + n)pi)/(m + n))`

with

`1/pi(Sin((m - n) pi)/(m - n) + Sin((m + n)pi)/(m + n)) = 0` for `n ne m` and

`int_-1^1 cos^2(n pi x) dx =1 + Sin(2 n pi)/(2 n pi)`

and also

#int_-1^1 x^2 cos(npi x) dx = (4 n pi Cos(n pi) + 2 (n^2 pi^2-2) Sin(n pi))/(n^3 pi^3)#

so finally

`(int_-1^1 x^2 cos(npi x) dx)/(int_-1^1 cos^2((k pix) dx)) = a_k`

so `a_k = (4Cos(kpi) )/(k^2 pi^2)`

with `a_0 =1/2int_-1^1 x^2 dx`

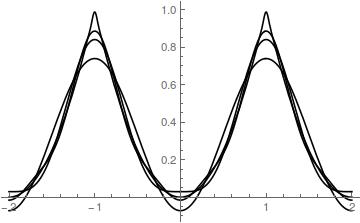
Attached a plot representing some mild approximations