We're looking for a bound #k# such that the area under the standard normal curve between #-k# and #k# is 0.95. This means that the tails should have the remaining 0.05 area, and since the tails are symmetric, the upper tail should have area 0.025. And if the upper tail has area 0.025, then the total area not in that upper tail should be the other 0.975.
In math terms:
#"P"("–"k < Z < k)=0.95#
#<=>"P"(Z<"–"k)+"P"(Z>k) = 0.05#
#<=>"P"(Z>k) = 0.025#
#<=>"P"(Z<=k)=0.975#
This final equation is asking, what #z#-coordinate on the standard normal curve has a cumulative probability of 0.975? This is found by reverse-lookup in a #z#-table. Find a cell in a #z#-table that is as close to 0.975 as you can, then the #k# value you want is the row & column that cell is in.
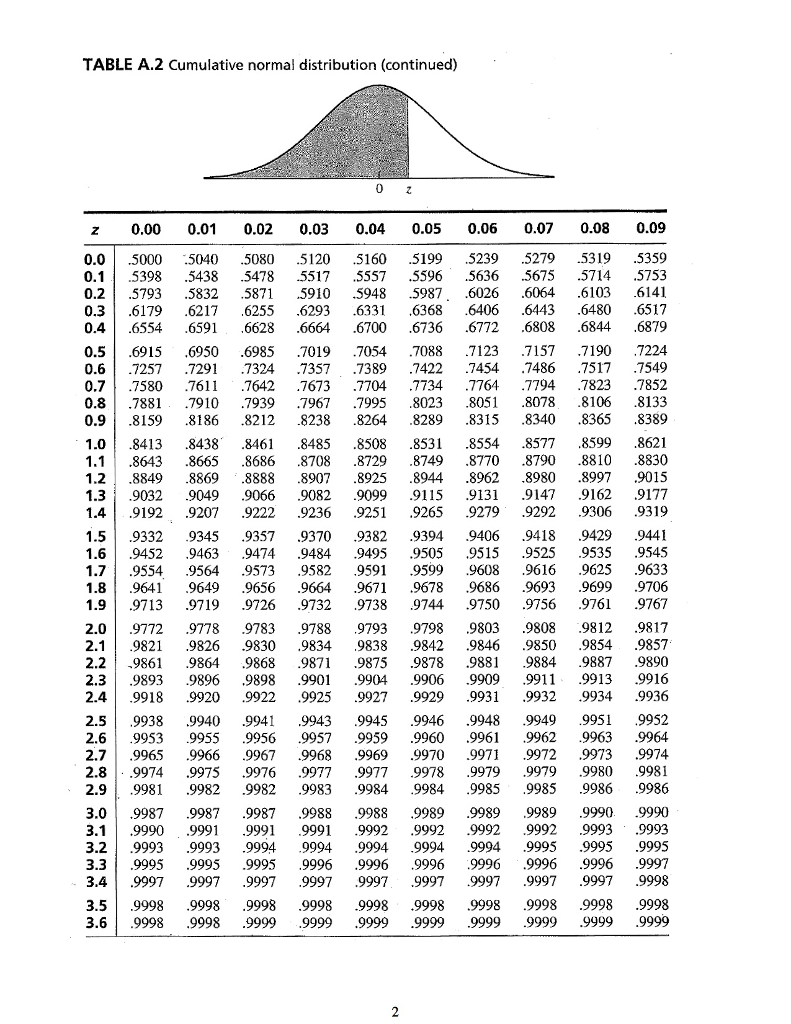
Because a region of area 0.95 is used very often in statistics, many of us know by heart that #k~~1.96# is the answer.


