Question

Question #7b342

Answer 1

`Delta W = ((7.51cm+7.08cm)/7.51cm)^2*4.4J-4.4J=12J`

Explanation:

There are at least 2 ways to answer this question: 1 equations and substitution, 2. graphically. I'm going to do both, here I'll start with graphing.

We start by noting that work is equal to force multiplied by the distance over which it is applied:

`W=F*d`

In this question, the force is being applied to a spring as it stretches, starting at it's unstressed length where the force is zero. This means that the force is constantly changing such that the work per unit distance is increasing as the spring stretches and the force increases. We can rewrite the equation above to account for this:

`W=F(x)*x`

Where we have taken the distance as the `x` coordinate. We can draw a graph of the force vs. distance and it becomes clear that the work is the area of a triangle.

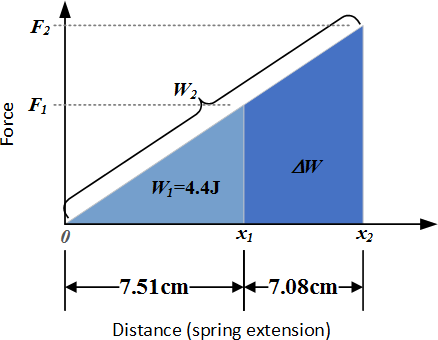
We know from the question that `x_1 = 7.51cm` and `W_1 = 4.4J`. The additional distance `Delta x = 7.08cm` and we are looking for the additional work `Delta W`.

We can use similar triangles to solve this problem, where we know the area of the smaller triangle is `W_1 = 4.4J`. The area of the larger triangle is `W_2` and we would like to know `Delta W = W_2 - W_1`.

The area of similar right triangles scales as the square of the ratio of the triangles. This is simple to see from the formula for the area of a right triangle:

`W_1 = 1/2 x_1*F_1`

Both the base and the height scale with the same ratio, `a`, for similar triangles giving:

`W_2 = 1/2 x_2 * F_2 = 1/2 (a*x_1)*(a*F_1) = a^2 *1/2 x_1*F_1`

`W_2 = a^2*W_1`

where

`a= x_2/x_1 = (x_1+Delta x)/x_1`

Finally, we can get:

`Delta W = W_2 - W_1=a^2*W_1-W_1`

`Delta W = ((x_1+Delta x)/x_1)^2*W_1-W_1`

`Delta W = ((7.51cm+7.08cm)/7.51cm)^2*4.4J-4.4J = 12J`

Answer 2

`Delta W = (4.4J*(7.51cm+7.08cm)^2)/((7.51cm)^2)*-4.4J`

`Delta W = 12J`

Explanation:

There are at least 2 ways to answer this question: 1 equations and substitution, 2. graphically. I'm going to do both, here I'll start with equations and substitution.

We start by noting that work is equal to force multiplied by the distance over which it is applied:

`W=F*d`

In this question, the force is being applied to a spring as it stretches, starting at it's unstressed length where the force is zero. This means that the force is constantly changing such that the work per unit distance is increasing as the spring stretches and the force increases. We can rewrite the equation above to account for this:

`W=F(x)*x`

Where we have taken the distance as the `x` coordinate. We can draw a graph of the force vs. distance and it becomes clear that the work is the area of a triangle.

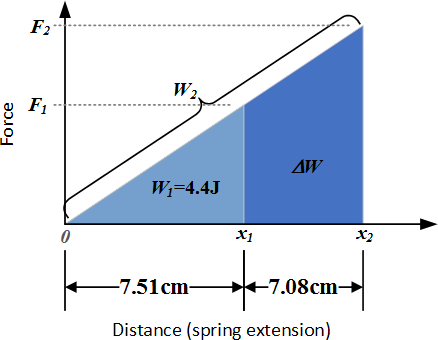
The equation for work is then:

`W_1 = 1/2 x_1*F_1` `color(white)(" ")(1)`

`W_2 = 1/2 x_2*F_2 = 1/2 (x_1+Delta x)*F_2` `color(white)(" ")(2)`

`DeltaW = W_2-W_1` `color(white)(" ")(3)`

We also know the equations for the force that must be applied to the spring:

`F(x) = k*x`

where `k` is the spring constant. This gives us expressions for the forces at the two points of interest:

`F_1 = k*x_1` `color(white)(" ")(4)`

`F_2 = k*x_2 = k*(x_1+Delta x)` `color(white)(" ")(5)`

Let's eliminate `k` by solving `(4)` for `k` and substituting into `(5)`

`F_2 = F_1/x_1*(x_1+Delta x)` `color(white)(" ")(6)`

Now we'll use `(1)` to solve for `F_1` and substitute into `(6)`

`F_2=(2*W_1)/x_1^2*(x_1+Delta x)` `color(white)(" ")(7)`

Finally, we substitute `(7)` into `(2)` and then into `(3)` to get

`Delta W = (W_1*(x_1+Delta x)^2)/x_1^2*-W_1`

`Delta W = (4.4J*(7.51cm+7.08cm)^2)/((7.51cm)^2)*-4.4J`

`Delta W = 12J`