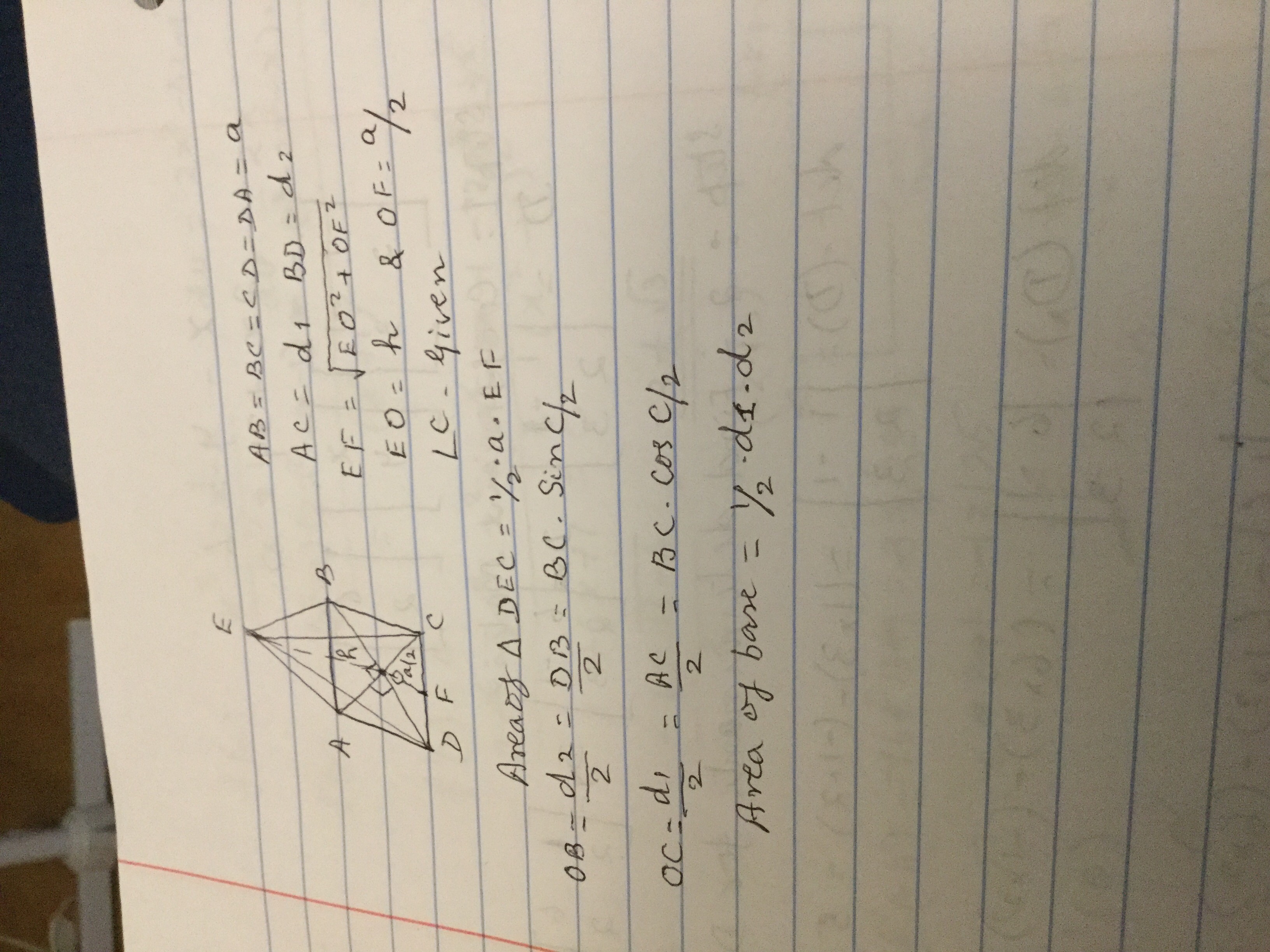A pyramid has a base in the shape of a rhombus and a peak directly above the base's center. The pyramid's height is #3 #, its base has sides of length #2 #, and its base has a corner with an angle of # pi/4 #. What is the pyramid's surface area?
1 Answer
Dec 6, 2017
T S A = 19.0133
Explanation:
AB = BC = CD = DA = a = 2
Height OE = h = 3
OF = a/2 = 1/2 = 1
Area of
Lateral surface area
diagonal
#OB = d_2/2 = BCsin (C/2)=3sin(pi/8)= 1.1481
#OC = d_1/2 = BC cos (C/2) = 3* cos (pi/8) = 2.7716
Area of base ABCD
T S A
T S A