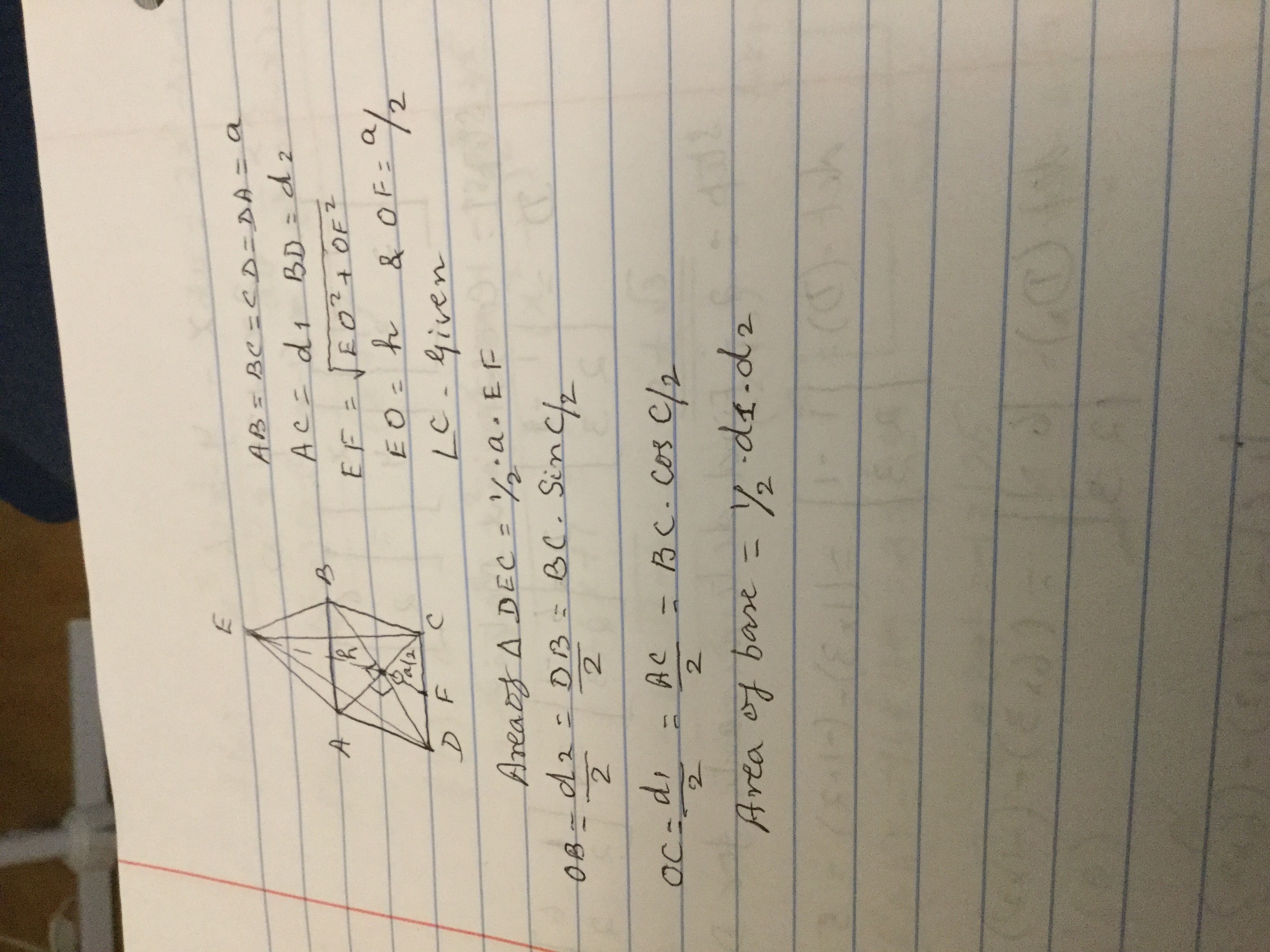A pyramid has a base in the shape of a rhombus and a peak directly above the base's center. The pyramid's height is #7 #, its base's sides have lengths of #5 #, and its base has a corner with an angle of #(5 pi)/8 #. What is the pyramid's surface area?
1 Answer
Dec 6, 2017
T S A = 97.4271
Explanation:
AB = BC = CD = DA = a = 5
Height OE = h = 7
OF = a/2 = 1/2 = 2.5
Area of
Lateral surface area
diagonal
#OB = d_2/2 = BCsin (C/2)=5sin((5pi)/16)= 4.1573
#OC = d_1/2 = BC cos (C/2) = 5* cos ((5pi)/16) = 2.7779
Area of base ABCD
T S A
T S A