Question

Question #d1df7

Answer 1

(a) 0.25 m

Explanation:

Time period = 1.6 s
Angular frequency, `omega = (2π)/T = 3.927` rad s⁻¹

Since we know the object passes the equilibrium with a velocity of 1.0 m s⁻¹ that is the object's maximum velocity.

Use this equation to solve the problem:
`v_(max) = omega A`

`A = v_(max) / omega = 1.0/3.927 = 0.2546` m

So the answer is (a)

Answer 2

Option ( B)

Explanation:

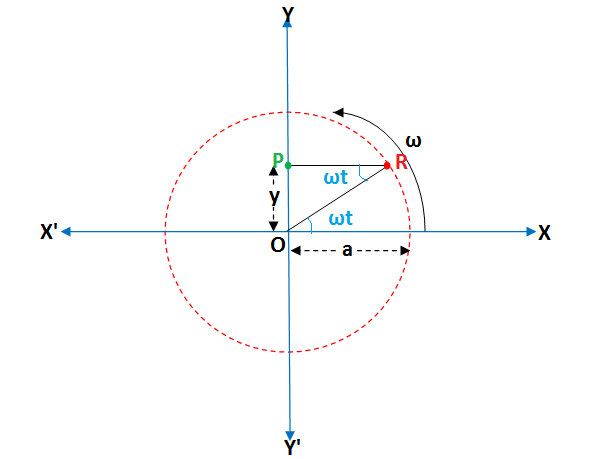
Let the object `color(green)(P)` executes SHM on Y-axis maintaining its equilibrium position at origin O . Given that the time period of oscillation is `T=1.6`s. The angular velocity `omega` of the reference point `color(red) (R)` associated with SHM undergoing uniform circular motion will be given by `omega=(2pi)/T=(2pi)/1.6"rad/s"`.

Considering that time count is started when the object is at origin. So we can write the equation for displacement `x` in t sec as

`color(red)(y=asinomegat.....[1])` , where `a` is the amplitude of vibration

Here origin is also its equilibrium position and It returns repeatedly to this position after each complete oscillation for 1.6s.

So the velocity `v` of the object after `t` sec will be obtained by differentiating the above equation w r to t

`color(blue)(v=(dy)/(dt)=aomegacosomegat.......[2])`

Now it is given that the velocity of the object after passing the equilibrium position by `0.2`s is `1m"/s"`

So we can insert `t=0.2`s, `v=1m"/s"` in [2] to find out `a`

`v=aomegacosomegat`

`1=axx(2pi)/1.6xxcos((2pi)/1.6xx0.2)`

`=>1=axx(2pi)/1.6xxcos(pi/4)`

`=>1=axx(2pi)/1.6xx1/sqrt2`

`=>a=(0.8xxsqrt2)/pi~~0.36m`