First we need to layout our points in a diagram so that we can begin to solve the problem:
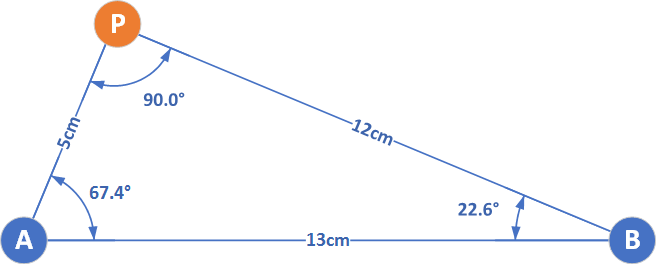
Where we have used the law of cosines to solve for each of the angles, knowing the length of the sides. We can then focus on the point P, making that our origin and choosing the x-axis direction the same as the line joining A to B:
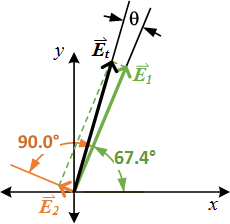
We can now solve for the contributions to the total electric field, #vecE_t#. We'll call the field from #q_1 -> vecE_1# and the field from #q_2 -> vecE_2#.
#vecE_1 =1/(4 pi epsilon_o) q_1/r_(AP)^2 hatr_(AP)#
where #r_(AP)# is the distance from point A to P and #hatr_(AP)# is a unit vector pointing in the direction from A to P.
#vecE_1 =(N*m^2)/(4 pi 8.85xx10^(-12)C^2) (8xx10^-6C)/(0.05m)^2 hatr_(AP)#
#vecE_1 = 2.88xx10^7N/C hatr_(AP)#
similarly,
#vecE_2 =1/(4 pi epsilon_o) q_2/r_(BP)^2 hatr_(BP)#
#vecE_2 =(N*m^2)/(4 pi 8.85xx10^(-12)C^2) (5xx10^-6C)/(0.12m)^2 hatr_(BP)#
#vecE_2 = 3.12xx10^6N/C hatr_(BP)#
We know from the work we did to find the angles in the triangle, that the angle between #vecE_1# and #vecE_2# is #90^o#, so the resultant vector when we add these two is the hypotenuse of the triangle that they form. Therefore the length of the resultant field vector is:
#abs(vecE_t)=sqrt(abs(vecE_1)^2+abs(vecE_2)^2)#
#abs(vecE_t)=sqrt((2.88xx10^7N/C)^2+(3.12xx10^6N/C)^2)#
#abs(vecE_t)=2.90xx10^7N/C#
Finally, to get the direction of the resultant, we need the angle #theta# from our diagram:
#theta=arctan(abs(vecE_1)/abs(vecE_2))=arctan((3.12xx10^6N//C)/(2.88xx10^7N//C))#
#theta = 6.2^o#
Therefore the angle that the resultant makes from the x-axis is:
#angle vecE_t=theta + 67.4^o = 73.6^o#
Putting it all together, the resulting electric field is:
#vecE_t = 2.90xx10^7N/C angle 73.6^o#



