What is the area?
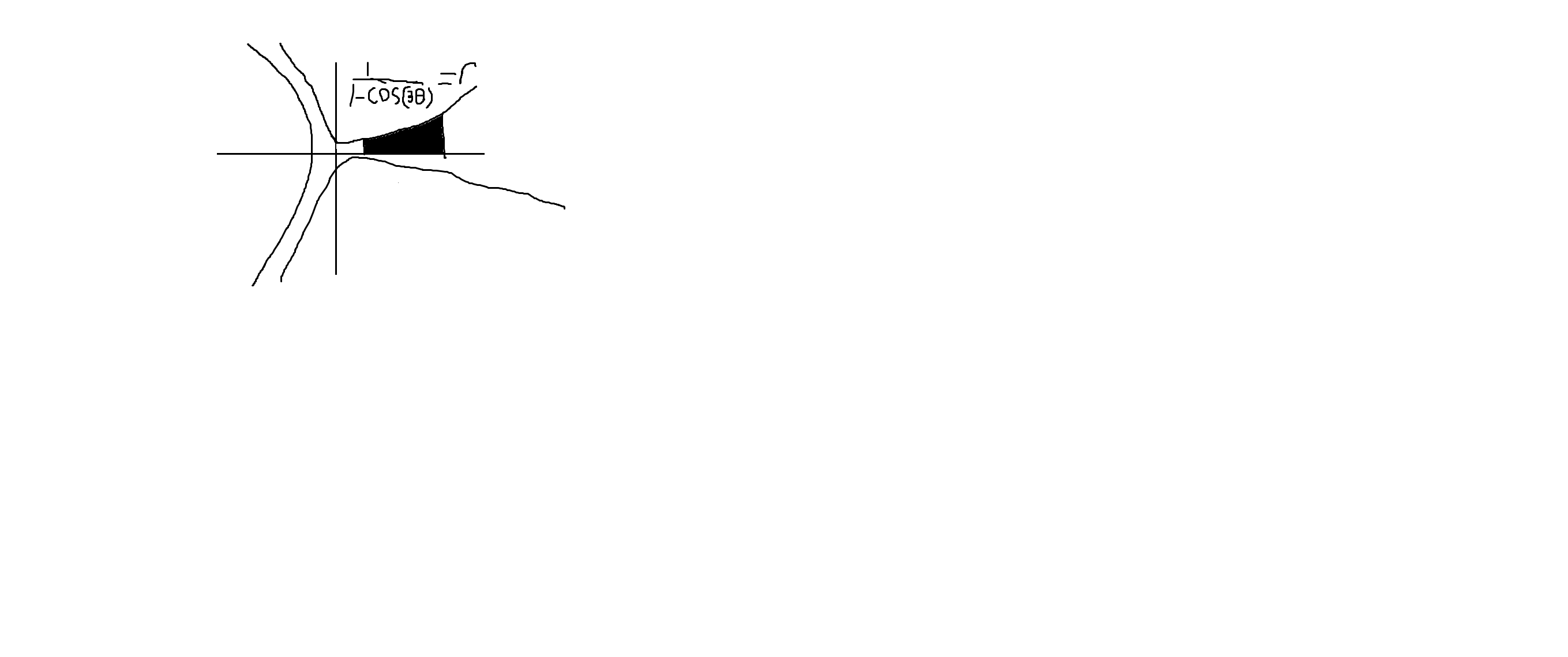
2 Answers
There is no real solution to this question.
Explanation:
The integral is not valid, if you look at what happens when theta approaches 0, you will see the function goes large, thus the area between [0,1] is kind of infinity.
---by @miles-a
I'm sorry. I don't know the steps of solving this. But you can try the formula mentioned by @alvin-l-2 as the following.
The calculation is hard. I used http://www.wolframalpha.com/ and obtained the result(about
Explanation:
This is the graph of
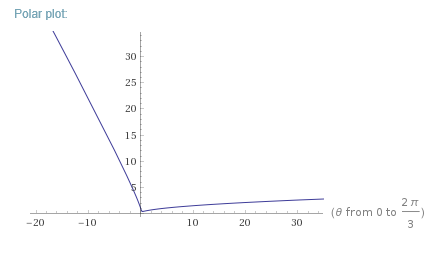 http://www.wolframalpha.com/input/?i=polar+r%3D1%2F(1-cos(3theta))
http://www.wolframalpha.com/input/?i=polar+r%3D1%2F(1-cos(3theta))
Then, how to interpret the graph?
[1] The graph crosses
[2] When does the graph cross
To solve this, apply the formula
Use the formula
The real solution for this is:
In cartesian form, the graph crosses
Now we are ready to calculate the area.
The area bounded by polar curves is
In this problem,
However, this integration is done in polar coordination. You must add the area of the right triangle with vertices(in cartesian form)
The answer is
By the way, calculating areas bounded by polar curves is so difficult. I don't think it is necessary for us to do these types of calculation without a calculator.
I posted a question https://socratic.org/questions/calculating-areas-bounded-by-polar-curves-looks-extremely-difficult-do-americans two months ago but nobody has answered this. What are your opinions?


