Question

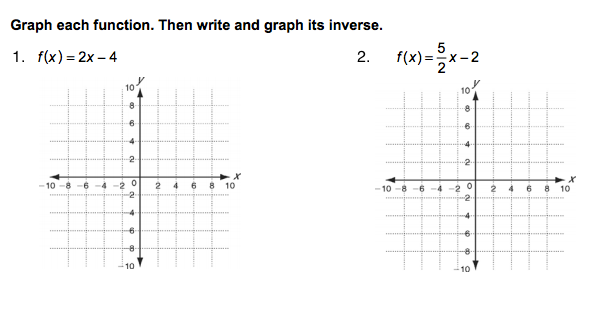
Image attached. Please help?

Answer 1

Find the inverse and then graph.

Explanation:

`f(x)=2x-4`

To find an inverse, switch `x` and `y` and then solve for the "new" `y`.

`f(x)=2x-4` can be written as `y=2x-4`

Switch `x` and `y`.

`x=2y-4`

Solve for the "new" `y`.

`x color(white)(xxxx)=2y-4`
`color(white)(x)+4color(white)(xxxxx)+4color(white)(xxxx)`Add 4 to both sides.

`x+4=2y`

`(x+4)/2=(2y)/2color(white)(xxxx)`Divide both sides by 2.

`y=(x+4)/2 = 1/2x +2`

Rewrite in function notation. `f^(-1)(x)` is the symbol for inverse.

`f^(-1)(x)=1/2x+2`

The graph of the original function is shown below.
graph{2x-4 [-10.04, 9.96, -7.4, 2.6]}

The graph of the inverse is shown below. Note that the inverse can also be drawn by finding some points on the original graph, and switching x and y. For example, the original graph goes through `(0,-4)` and the inverse goes through `(-4,0)`.

graph{1/2x +2 [-10.21, 9.79, -3.36, 6.64]}

For the second problem, `f(x)=5/2x-2`, first switch `x` and `y`.

`x=5/2y-2`

Solve for the new `y`.

`xcolor(white)(xxx)=5/2y-2`
`color(white)(x)+2color(white)(xxxxx)+2`

`x+2=5/2y`

`2/5(x+2)= 2/5*5/2y`

`y=2/5x +4/5color(white)(xxx)`or`f^(-1)(x) =2/5x +4/5`

This answer is lengthy, so I'll skip the graphs of the second problem.