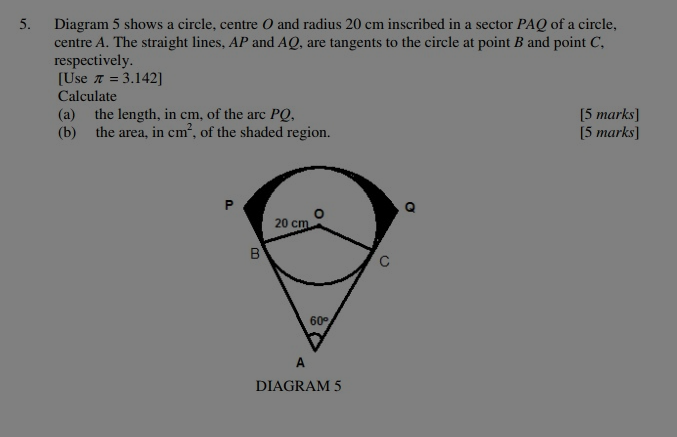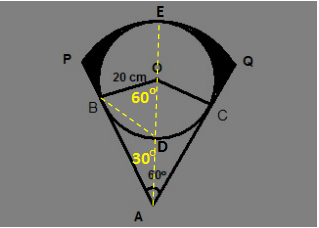
#AandO# are joined and produced up to E ,the point of contact of the circle of center O with the sector PAQ.#B andD# are also joined.
Now #AP=AQ=AE="radius of the sector "PAQ#
Given that AB and AC are two tangents from A to the circle of center O. we can say #AB=AC# and the two right triangles #OAB and OAC# are congruent . So #/_BAO=/_CAO=30^@#
As it is given #/_BAC=60^@# we get
#/_BAO=/_CAO=30^@# So we have #/_AOD=60^@#
Now in #Delta AOD,OB=OD and /_BOD=60^@#. So it is an equilateral triangle So #OB=OD=BD=20cm#
Thus #/_BDA=180^@-/_BDO=180^@-60^@=120^@#
Hence #/_DBA=180^@-120^@-30^@=30^@#
So #Delta ABD# is isosceles
Hence
#AD=BD=OD=20cm#
Hence radius of the sector PAQ is #AE=3xx20cm=60cm#
a) Now #"arc"PQ=pi/180^@xx60^@xx"Radius" AE#
#=pi/3xx60cm=20pi" "cm#
b) The area of the shaded region
#="Area of sector PAQ"-" Area of the sector BECO"-"area of " 2DeltaOBA#
#=60^@/360^@xxpi60^2-240^@/360^@*pi20^2-2*1/2xxABxxBO#
#=1/6pi60^2-2/3pi20^2-BO^2cot30^@" "cm^2#
#=354.38" "cm^2#