How do I identify the symmetry of the graph #(3x^2)+(3y^2)=5#?

Question

1621 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-12-17T14:59:59

#x= 0 #

#y = mx , m in RR#

( #m# can be any real value )

We can see by dividing by #5#:

#x^2 + y^2 = 5/3 #

#=> x^2 + y^2 = (sqrt(5/3))^2#

We know the general equation of a cirlce:

#x^2 + y^2 = R^2 # is a cirlce of centre #(0,0)# of radius #R#

Hence this is a circle of radius, #sqrt(5/3) #

A sketch:

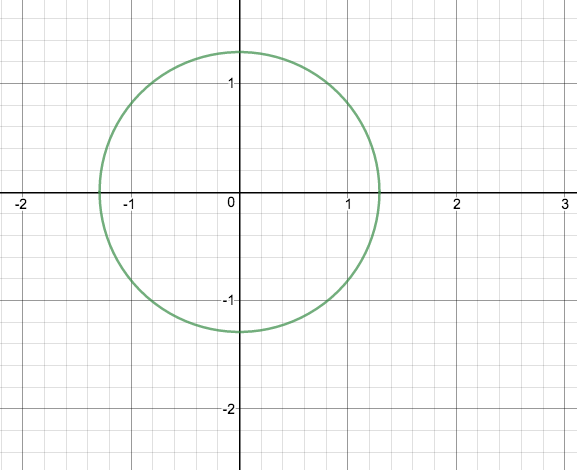
enter image source here

We can imediately see that when flipped in the #x# and #y# axis, it stays the same:

# y = 0 , x = 0 # are the first two lines of symmetry we can see

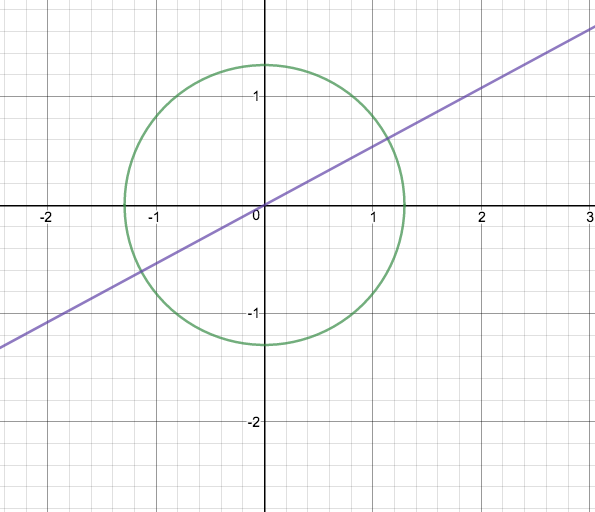
enter image source here

We can also see by this sketch, that any line of the equation #y = mx # is a line of symetry, as when fliped, it stays the same

#=> y = mx , m in RR # are also lines of symmetry

Answer 2 · 2017-12-17T23:40:29

It is a circle, so has symmetry group #O(2)#

Given:

#3x^2+3y^2=5#

Divide both sides by #3# to find:

#x^2+y^2 = 5/3#

That is:

#(x-0)^2+(y-0)^2 = (sqrt(15)/3)^2#

The standard form of the equation of a circle with centre #(h, k)# and radius #r# is:

#(x-h)^2+(y-k)^2 = r^2#

So we can see that the given equation is that of a circle with centre #(h, k) = (0, 0)# and radius #r=sqrt(15)/3#

graph{x^2+y^2=5/3 [-4.4, 4.4, -2.2, 2.2]}

This has reflective symmetry about any line through the centre.

It also has rotational symmetry by any angle about the centre. In fact any rotation can be generated by a combination of two reflections.

The symmetry group of these reflections/rotations is called #O(2)# - the orthogonal group in two dimensions.