Equilateral triangle ABC has side length of 1, and squares ABDE, BCHI, CAFG lie outside the triangle. What is the area of hexagon DEFGHI?
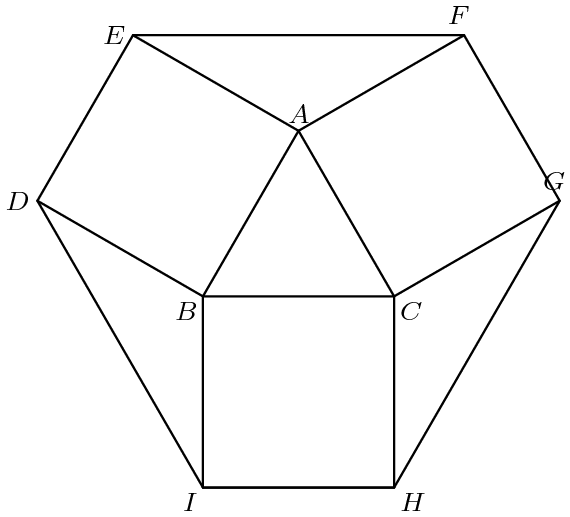
2 Answers
Explanation:
We will use, to find the Area of
Observe that
they all have the same Area,
Also, Area of the equilateral
Hence, The Area of the Hexagon
Area of hexagon
-
Area of
#Delta ABC#
Draw a line perpendicular from vertex#A# on side#BC# . This is altitude of the triangle#ABC# . This perpendicular also bisects#angle BAC# . As each side of equilateral triangle is#=1# and each angle#=60^@#
Altitude#=1xxcos30^@=sqrt3/2#
Area of#DeltaABC=1/2xx"base"xx"altitude"#
#=1/2xx1xxsqrt3/2=sqrt3/4# -
Area of three squares.
Each square has side#=1# and therefore has area#=1^2=1#
Total area of three squares#=3xx1=3# -
Area of three
#Delta# s#EAF, DBI, HCG#
For#DeltaEAF#
Note that in angle at#A=360^@#
This angle is equal to four angles#=60^@+90^@+90^@+angleEAF#
Equating both we get#angleEAF=360^@-240^@=120^@# .
Altitude of#DeltaEAF# can be found as explained in case of#Delta ABC# above
Altitude of#DeltaEAF=1xxcos60^@=1/2#
Half of side#EF=1xxsin60^@=sqrt3/2#
Base#EF=2xxsqrt3/2=sqrt3#
Area of#DeltaEAF=1/2xxsqrt3xx1/2=sqrt3/4#
Similarly area of other two triangles is also same.
Area of hexagon
