How do you convert #0.18bar(3)# to a fraction?
2 Answers
Explanation:
To convert a decimal to a fraction, you have to see how many places the decimal is. This chart may help: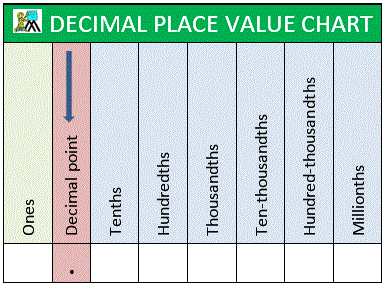
After you know what place the decimal ends at, you put the numbers after the decimal point over the place. For example, your decimal
If you were to have a full number with your decimal, it would stay a whole number in you fraction. For example, say I had
Your number is already in simplest form, but if you were to need to put a number in simplest form, you have to get the number to where the numerator and the denominator have no more common factors.
So:
I hope this makes sense. If you need more information on common factors and simplest form, go to
or
Explanation:
Given:
#0.18bar(3)#
Multiply by
#100(10-1) 0.18bar(3) = 183.bar(3)-18.bar(3) = 165#
Divide both ends by
#0.18bar(3) = 165/(100(10-1)) = (11*color(red)(cancel(color(black)(15))))/(60*color(red)(cancel(color(black)(15)))) = 11/60#
Why
The first multiplier


