Question

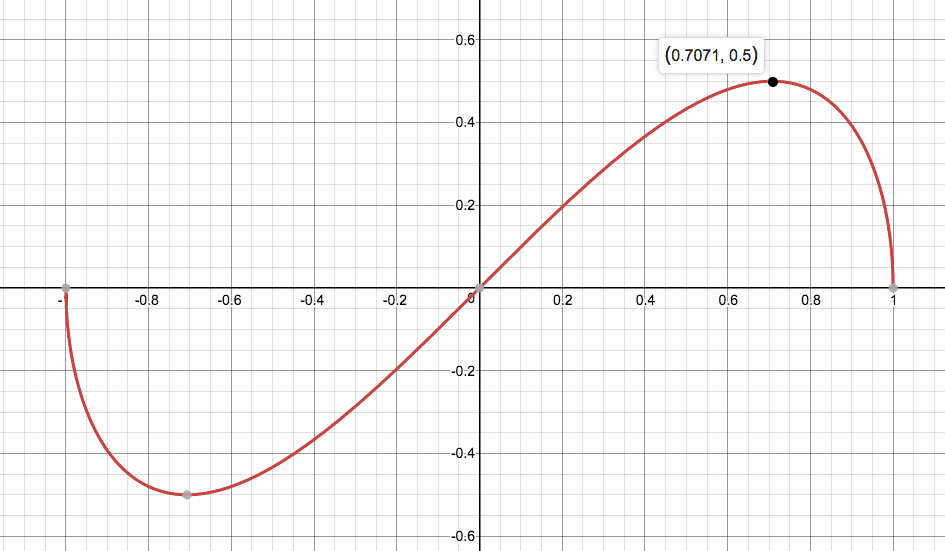
At what point or points on the circle `x^2+y^2=1` does `f(x, y)=xy` have an absolute maximum, and what is that maximum?

Answer 1

See below.

Explanation:

Making a change of variables

`x=r cos theta`
`y=r sin theta` and substituting

`f(x,y) -> g(r, theta) = r^2 cos theta sin theta`

and the restriction gives `r = 1`

so the problem is reduced to

`min sin theta cos theta`

for `0 le theta < 2pi`

Now `(dg)/(d theta) = cos(2theta) = 0` gives the stationary points. or

`theta = pm pi/4 +k pi` and the maximum is for `theta = pi/4` and consequently

`x = cos(pi/4), y = sin(pi/4)`

Answer 2

Absolute max `= 1/2`

Explanation:

I wanted to provide an alternate way of answering this problem...

We know `x^2 + y^2 = 1`

`=> y^2 = 1-x^2`

`=> y = sqrt(1-x^2 )`

So hence `f(x,y) = xsqrt(1-x^2 )`

Now to find the maximum we must set the differential to 0:

`-------------------`

We must use our knowledge of the chain and product rule:

`if y = uv , y' = udv + vdu`

`if y = f(g(x)) , y' = f'(g(x)) * g'(x)`

`-------------------`

`f'(x,y) = sqrt(1-x^2) + x*( 1/2 * (1-x^2)^(-1/2) * -2x )`

`f'(x,y) = sqrt(1-x^2) - (x^2)/sqrt(1-x^2)`

Setting `f'(x,y) = 0`:

`=> sqrt(1-x^2) - (x^2)/(sqrt(1-x^2)) = 0`

`=> sqrt(1-x^2) = (x^2)/(sqrt(1-x^2)`

`=> 1-x^2 = x^2`

`=> 1 = 2x^2`

`=> 1/2 = x^2`

`=> x = 1/sqrt2`

Using `y = sqrt(1-x^2)`:

`=> y = 1/sqrt2`

Max `xy => 1/sqrt2 * 1/sqrt2 = 1/2`

We can check that this is a maximum by taking `f''(x,y)` and verifying that at `x= 1/sqrt2` that `f''(1/sqrt2 ,y) < 0`

As `(d^2y)/(dx^2) < 0` means a maximum