How to find the modulus of a vector?

enter image source here
Can someone please explain to me how to do question 4 b iii) Thanks heaps!

2 Answers
Jim G.
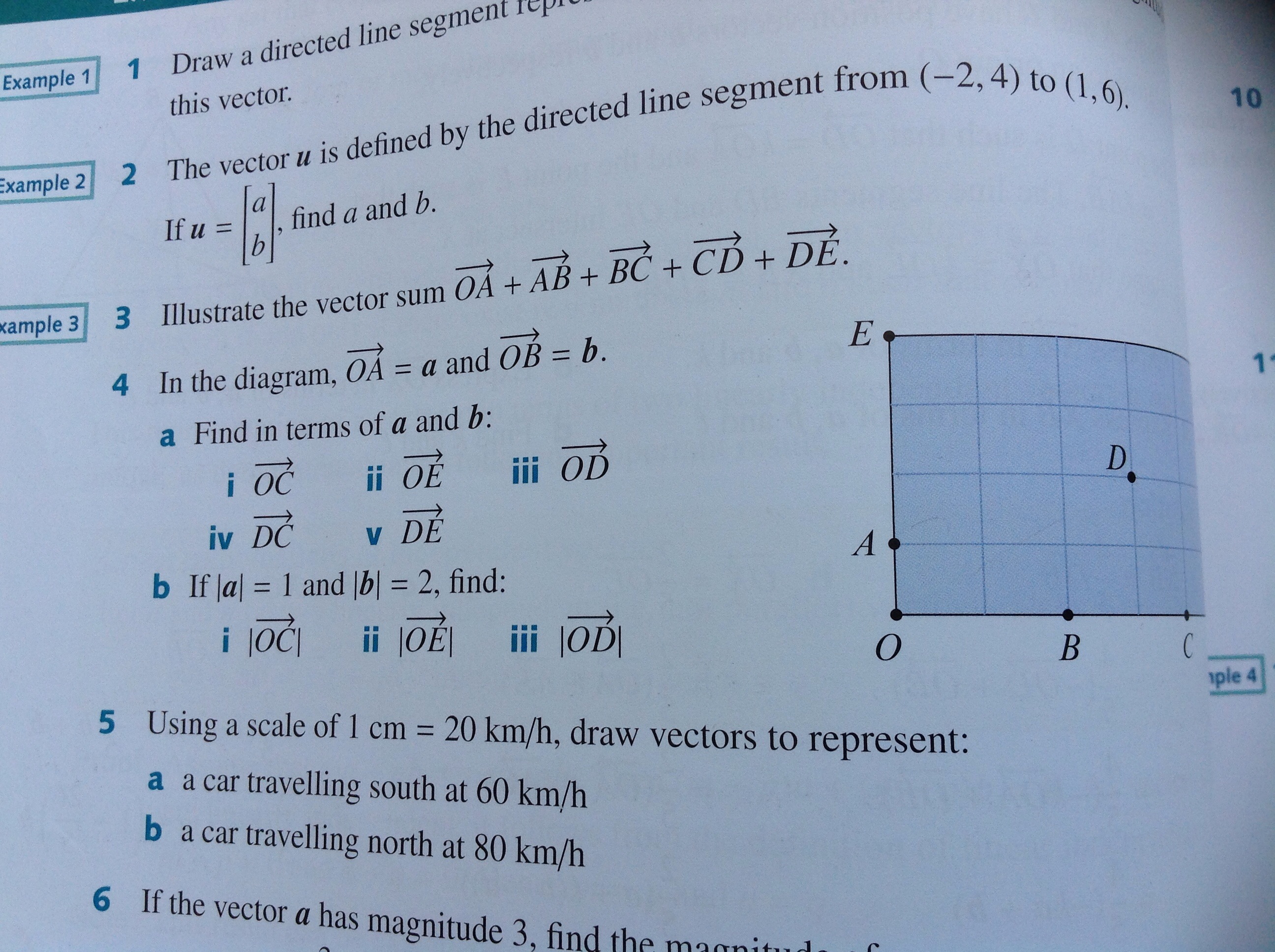
Dec 22, 2017

#|vec(OD)|=sqrt13#

Explanation:

#"given the vector "((x),(y))" then"#

#|((x),(y))|=sqrt(x^2+y^2)larrcolor(red)"magnitude of vector"#

#"here "vec(OD)=((3),(2))#

#rArr|vec(OD)|=sqrt(3^2+2^2)=sqrt13#

Rhys
Dec 22, 2017

#|OD| = sqrt(13) #

Explanation:

To understand this problem we must first know what modulus really means, in this case, the length of the vector...

So #|OD| # is just the length of the vector from #O# to #D#....

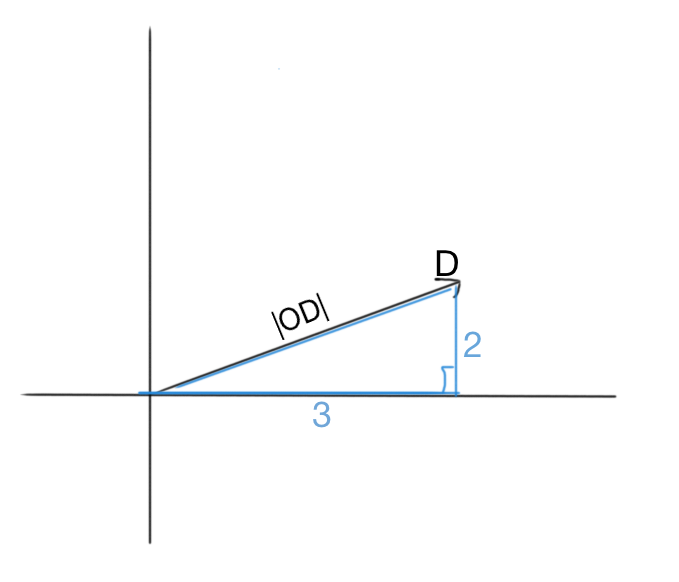
enter image source here

We can see that we can form a right angle triangle, with sides #2 and 3 #, so to find #|OD| # we can use pythagerous' theorem:

#a^2 + b^2 = c^2 #

#=> |OD|^2 = 3^2 + 2^2 #

#=> |OD|^2 = 13 #

#=> sqrt( |OD|^2 ) = sqrt(13) #

#=> |OD| = sqrt(13) #

Related questions
Impact of this question
42955 views around the world
You can reuse this answer
Creative Commons License