Question

What are the values and types of the critical points, if any, of `f(x,y) = x(2-x-y)`?

Answer 1

Saddle point at `(0,2)`

Explanation:

I will assume by "critical points" you are referring to the values of `x` and `y` where the function is stationary.

First we need to find the partial derivatives of the function:

The `x` partial derivative:

`(partialf)/(partialx) = (2-x-y)+x(-1) = 2-x-y-x`
`=2-2x-y`

by use of the chain rule.

The `y` partial derivative:

`(partialf)/(partialy)=x(-1)=-x`

We now take both of these equations, and set them equal to 0 to obtain a pair of simultaneous equations which can then be solved to obtain one or more pairs of co-ordinates where our stationary point lies, so:

`2-2x-y=0`
`-x=0`

Immediately we can obviously see `x=0` from the bottom equation. That leaves us with:

`2-y=0`

for the top equation. This has the solution:

`y=2`

So we have only one stationary point at `(0,2)`. Here `f(0,2)=0`

In order to classify the point we now need to find the higher order derivatives, those will be:

`(partial^2f)/(partialx^2)=-2`
`(partial^2f)/(partialy^2)=0`
`(partial^2f)/(partialxpartialy)=-1`

We can classify the points by:

`(partial^2f)/(partialx^2)(partial^2f)/(partialy^2)-((partial^2f)/(partialxpartialy))^2 < 0` at `(x,y)`

then it will be a saddle point, or else if:

`(partial^2f)/(partialx^2)(partial^2f)/(partialy^2)-((partial^2f)/(partialxpartialy))^2 >0` as `(x,y)`

then it will be a maximum or minimum. Substituting the values of our derivative in we get:

`(2)(0)-(-1)^2=-1<0` So it is a saddle point. Hence our critical point is a saddle point at `(0,2)`.

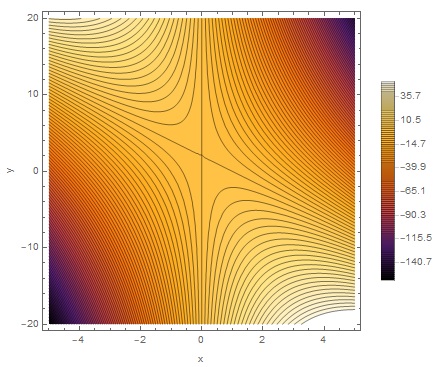
I have included a contour plot of the function below (I did try a 3d plot at first but the shallowness of the gradient did not make the turning point clear enough). On the image the darker regions represent values of low `f(x,y)` and the brighter regions represent high `f(x,y)` in accordance with the plot legend.

We see that going from the bottom left to the top right you go up "over a hill" reaching a maximum at the calculated stationary point. Similarly going from the top left to the bottom right you go through the "bottom of a valley" with the minimum being at the calculated stationary point.

In other words, we notice that the contours from all directions converge at `(0,2)`, hence the stationary point of the function. Hopefully this helps to see the idea more clearly.