Question

How do you find the tangent lines to this circle `x^2 + y^2 – 10x + 8y - 8 = 0` passing through the point A (-2,3)?

Answer 1

Here is a graph of the circle and the point:

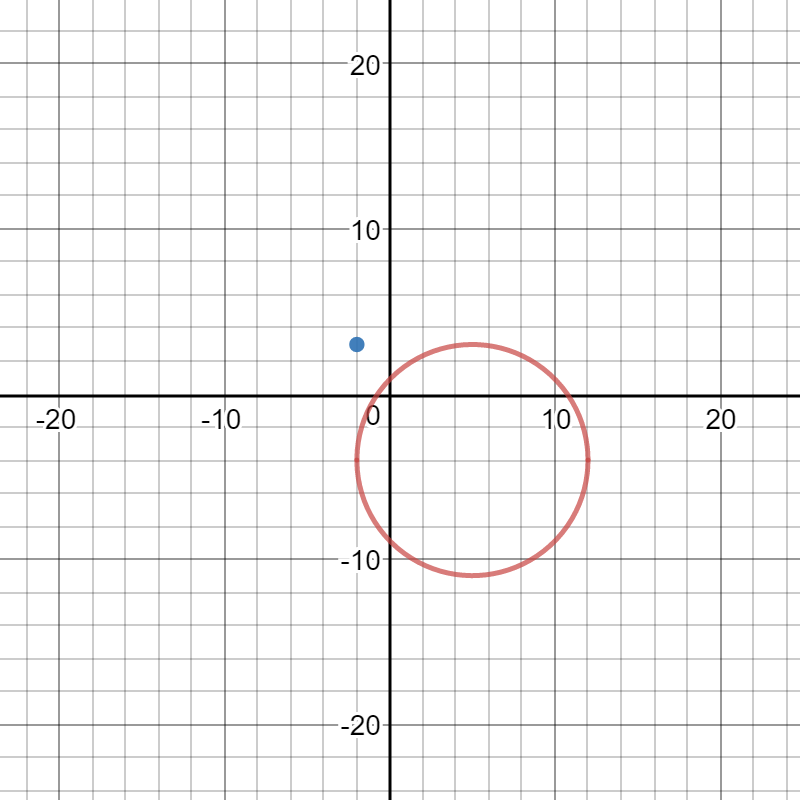
Please observe that the point does not lie on the circle.

We need to complete the squares so that we have the standard Cartesian form:

`(x-h)^2+(y-k)^2= r^2`

`x^2 + y^2 – 10x + 8y = 8`

`x^2 -10x+h^2 + y^2 + 8y+k^2 = 8+h^2+k^2`

`-2hx=-10x`

`h=5`

`(x -5)^2 + y^2 + 8y+k^2 = 8+5^2+k^2`

`-2ky = 8y`

`k=-4`

`(x -5)^2 + (y - (-4))^2 = 8+5^2+(-4)^2`

Combine the constant terms and mark as equation [1]:

`(x -5)^2 + (y - (-4))^2 = 49" [1]"`

The point-slope form of a line through the point `(-2,3)` is:

`y = m(x+2)+3`

Distribute m and mark as equation [2]:

`y = mx +2m+3" [2]"`

Substitute equation [2] into equation [1]:

`(x -5)^2 + (mx +2m+3 -(-4))^2 = 49`

Combine like terms within the second square:

`(x -5)^2 + (mx +2m+7)^2 = 49`

Expand the squares

`x^2 -10x+25 + m^2 x^2 + (14 m + 4 m^2) x + 49 + 28 m + 4 m^2 = 49`

Combine like terms:

`(m^2+1)x^2+ (4m^2+14m-10)x+4m^2+28m+25=0`

We want the values of m that make the above equation have only 1 corresponding value of x; the means that the discriminant must equal 0:

`b^2-4(a)(c) = 0`

`(4m^2+14m-10)^2 - 4(m^2+1)(4m^2+28m+25) = 0`

An obvious root is `m = 0`:

`(-10)^2 - 4(1)(25) = 0`

`100 - 100 = 0`

This is the horizontal line:

`y = 3`

By symmetry, the other slope must be undefined; implying the vertical line:

`x = -2`

Let's confirm this graphically:

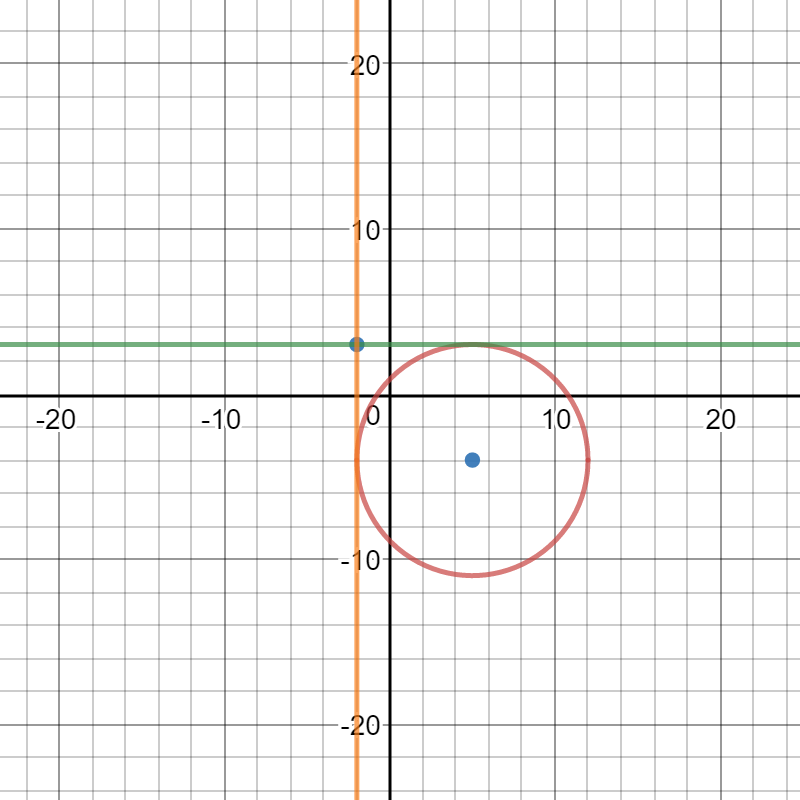
Confirmed! The equation of the tangent lines are:

`y = 3` and `x = -2`

NOTE: We could have obtained these answers by observing that the radius of the circle is 7 but this would have prevented me from showing you how to use `b^2-4(a)(c)=0` to find the values of m, when the numbers are not so nice.

Answer 2

`y-3=0, and x+2=0`.

Explanation:

Let `S : x^2+y^2-10x+8y-8=0` be the given circle. Then,

rewriting it as `S : (x-5)^2+(y+4)^2=7^2`, shows that,

the Centre `C` and Radius `r` of `S` are, `C(5,-4), and, r=7`.

For `A(-2,3), CA^2=(5-(-2))^2+(-4-3)^2=98 gt r^2`.

This means that the point (pt.) `A` is outside `S,` so that, there are

`2` tangents (tgts.) through `A`.

If `m` is the slope of the tgt., then, its equation (eqn.) is given by,

`t : y-3=m(x-(-2)), or, mx-y+(3+2m)=0.`

From Geometry we know that, the `bot"-distance"` from the

centre to the tgt. equals the radius.

But, the `bot"-distance"` from the centre to the tgt. `t` is,

`|5m-(-4)+3+2m|/sqrt(m^2+1)=|7m+7|/sqrt(m^2+1)`; which is `7`.

`:. (7|m+1|)/sqrt(m^2+1)=7:. (m+1)^2=m^2+1, or, m=0`.

Hence, `t ; y-3=0`.

But we surely know that there are `2` tgts.

So, which can be the other tgt.?

Recall that, we have supposed that the slope of tgt. is `m`.

In other words, this means that we have taken it for granted

that the slope of tgt. exists.

Evidently, the other tgt. (which definitely exists ), must have the

undefined slope, i.e., must be the vertical line through `A`.

Clearly, this other tgt. is `t : x=-2, or, x+2=0`.

It is easy to verify that the tgts. `y-3=0, and x+2=0` touch

`S` at `(5,3) and (-2,-4)` resp.

Enjoy Maths.!

Answer 3

See below.

Explanation:

Using vectors.

Given a point `p_1` external to the circle

`C-> norm(p-p_0)= r`

we can trace two tangent lines to `C` passing by `p_1`

Let `L-> p = p_1+ lambda vec v` such line then

`C nn L rArr C@ L = 0 rArr norm(p_1-p_0+lambda vec v) - r = 0`

or squaring

`norm(p_1-p_0)^2+2lambda << p_1-p_0, vec v >> + lambda^2 norm(vec v)^2-r^2=0`

and then

`lambda = 1/(2 norm(vec v)^2)(-2 << p_1-p_0, vec v >> pm sqrt(4<< p_1-p_0, vec v >>^2-4 norm(vec v)^2(norm(p_1-p_0)^2-r^2)))`

but the tangency needs

`4<< p_1-p_0, vec v >>^2-4 norm(vec v)^2(norm(p_1-p_0)^2-r^2)=0`

now putting

`vec v = (m,1)`
`p_1-p_0 = (x_1-x_0,y_1-y_0)`

`((x_1-x_0)m+(y_1-y_0))^2-(m^2+1)((x_1-x_0)^2+(y_1-y_0)^2-r^2)=0`

and solving for `m` with

`p_1 = (-2,3)`
`p_0 = (5,-4)` and
`r = 7`

gives

`m=0` then the lines are

`L_1 -> (x,y) = (-2,3)+lambda(0,1)`
`L_2->(x,y)=(-2,3)+lambda(1,0)`

NOTE:

Choosing `vec v = (1,m)` instead the result would be also `m = 0`