Solving quation?
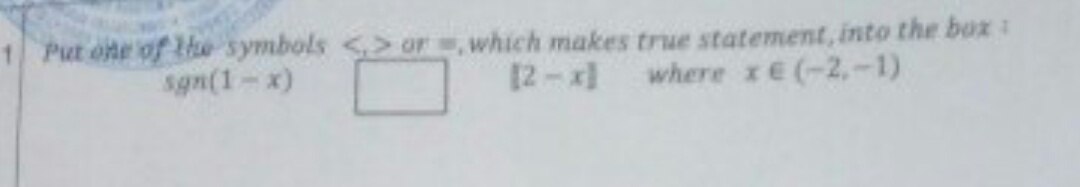
3 Answers
Explanation:
Explain: [According to Wikipedia] "sgn is an odd mathematical function that extracts the sign of a real number".
if
Because sgn is an ... that extracts the sign of a real number, in our case
Explanation:
Recall that, the Signum Function
Let us first modify the defn. of
Now,
If
On the similar lines,
For
Multiplying this inequality by
Now adding
Thus, since
Further,
Clearly,
We compare
Enjoy Maths.!
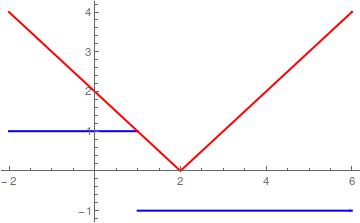
Explanation:
In blue the
As can be depicted,