Question

There are n identical cards of type A, n of type B, n of type C, and n of type D. There are 4 persons that each have to receive n cards. In how many ways can we distribute the cards ?

So the order in which they receive the cards does not matter. All that matters is how many cards of each type (A, B, C, or D) each person has. Can this be expressed with combinations depending on the parameter n ?

Answer 1

See below for an idea on how to approach this answer:

Explanation:

I believe the answer to the question of methodology on doing this problem is that Combinations with identical items within the population (such as having `4n` cards with `n` number of types A, B, C, and D) falls outside the ability of the combination formula to calculate. Instead, according to Dr. Math at mathforum.org, you end up needing a couple of techniques: distributing objects into distinct cells, and the inclusion-exclusion principle.

I've read this post (http://mathforum.org/library/drmath/view/56197.html) that deals directly with the question of how to calculate this type of problem over and over again and the net result is that while the answer lies in there somewhere, I won't attempt to give an answer here. I'm hopeful one of our expert math gurus can step in and give you a better answer.

Answer 2

A counting program in C yields following results :

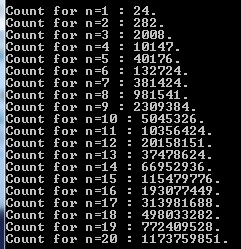
Explanation:

#include<stdio.h>

int main()
{
int n,i,j,k,t,br,br2,numcomb;
int comb[5000][4];
long count;

for(n=1;n<=20;n++)
{
numcomb = 0;
for(i=0;i<=n;i++) for(j=0;j<=n-i;j++) for(k=0;k<=n-i-j;k++)
{
comb[numcomb][0] = i;
comb[numcomb][1] = j;
comb[numcomb][2] = k;
comb[numcomb][3] = n-i-j-k;
numcomb++;
}
count = 0;
for(i=0;i<numcomb;i++)
{
for(j=0;j<numcomb;j++)
{
br = 0;
for(t=0;t<4;t++) if (comb[i][t]+comb[j][t]>n) br = 1;
if (!br)
{
for(k=0;k<numcomb;k++)
{
br2 = 0;
for(t=0;t<4;t++) if (comb[i][t]+comb[j][t]+comb[k][t]>n) br2=1;
if (!br2)
{
count++;
}
}
}
}
}
printf("\nCount for n=%d : %ld.", n, count);
}
printf("\n");
return(0);
}