Find a value of a so that the limit exists in a piece wise function?
I'm not sure how to start solving this problem.
For which value a does the lim(fx),x->5 exist where:
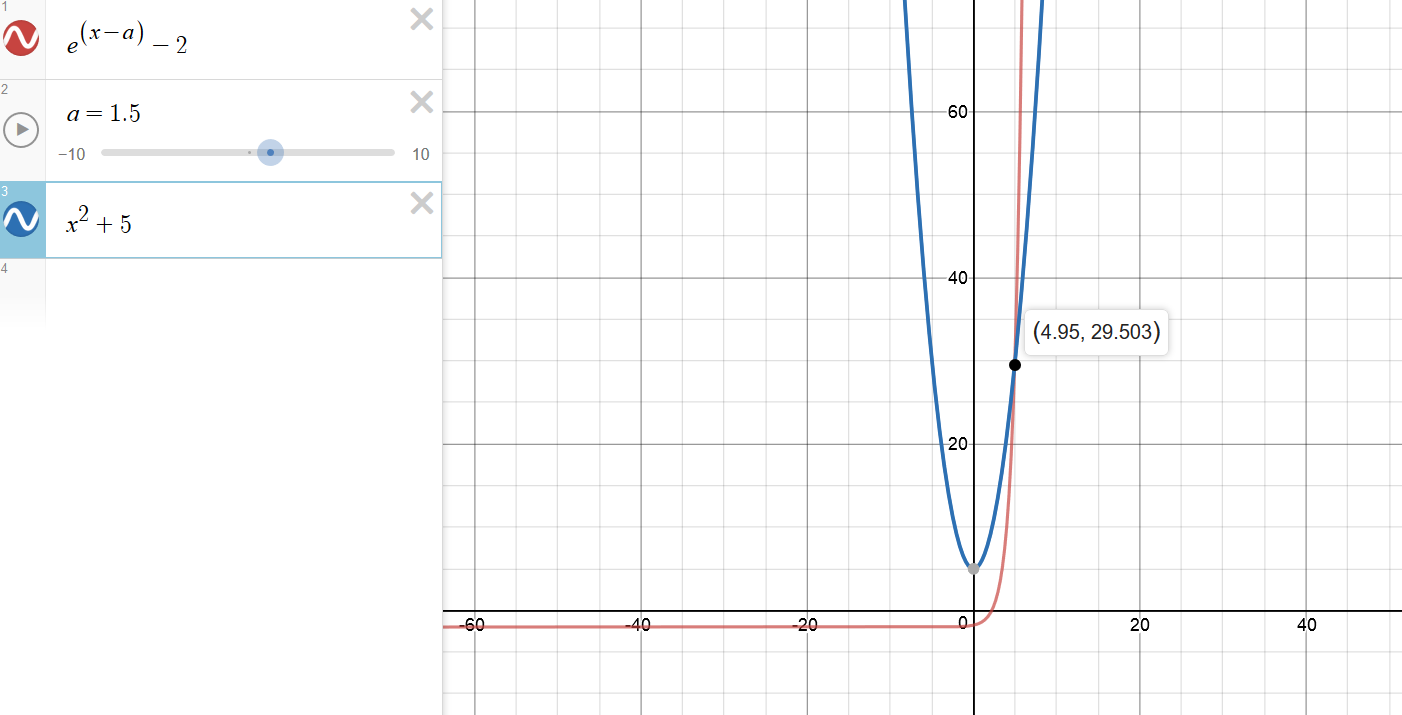
f(x) = { e^(x-a)-2 if x > 5, x^2+5 if x < 5
Anyone able to tell me where I should start?
I think maybe I set the two piecewise functions equal to each other and evaluate at x=5?
5-ln32 was the answer.
I'm not sure how to start solving this problem.
For which value a does the lim(fx),x->5 exist where:
Anyone able to tell me where I should start?
I think maybe I set the two piecewise functions equal to each other and evaluate at x=5?
5-ln32 was the answer.
2 Answers
Explanation:
Recall that,
Similarly,
Enjoy Maths.!
see explanation
Explanation:
Yes. The limit exist only when the value of a limit from right equals the value of a limit from left. That means we have to evaluate the value at the point x=5 from each function.
and as I said. These two results must equal:
To check the result I drew a graph. see below.(The closest value of a I could set is 1.5)