Question #6f0c5
1 Answer
See the explanation.
Explanation:
The equation of a plane is in the form
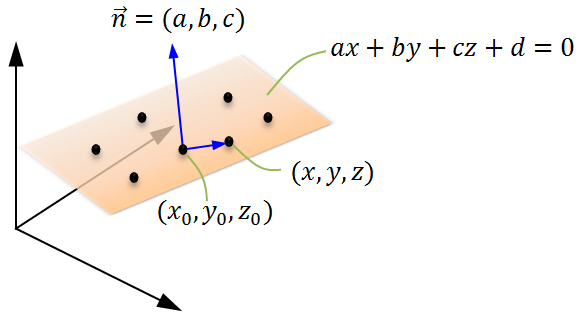
In the equation, the vector
However, there is no single equation
You have two options to express a 3-D line.
(A) Let
Then, the equation of the line using parameter
This is equivalent to the vector form

(B) Or, you can express the line as an intersection of two planes.
If you solve two equations of planes (of cource, they must not be parallel) as simultaneous equations, the root corresponds to the line.