Question

How do you find an equation of the tangent line to the curve at the given point `y=5cos(x)` and `x=pi/3`?

Answer 1

`y=-x((5sqrt(3))/2)+((5pisqrt(3)+15)/6)`

Explanation:

First we need to find the gradient at `x=pi/3`, since this will be the gradient of the tangent line. We need to calculate the first derivative.

`:.`

`d/dx(5cos(x))=-5sin(x)`

Gradient at `x=pi/3`

`f'(pi/3)=-5sin(pi/3)`

Slope point equation of a line.

`y-5cos(pi/3)=-5sin(pi/3)(x-pi/3)`

`y=-5xsin(pi/3)+((5pi)/3)sin(pi/3)+5cos(pi/3)`

Using identities:

`color(red)(sin(A-B)=sinAcosB-cosAsinB)`

`color(red)(cos(A-B)=cosAcosB+sinAsinB)`

`sin(pi/3)=sin(pi-(2pi)/3)=`

`->sin(pi)cos((2pi)/3)-cos(pi)sin((2pi)/3)=`

`->(0)(-1/2)-((-1)(sqrt(3)/2))=(sqrt(3))/2`

`cos(pi/3)=cos(pi-(2pi)/3)=`

`->cos(pi)cos((2pi)/3)+sin(pi)sin((2pi)/3)`

`->(-1)(-1/2)+(0)(sqrt(3)/2)=1/2`

`:.`

`y=-5xsin(pi/3)+((5pi)/3)sin(pi/3)+5cos(pi/3)`

`y=-5x((sqrt(3))/2)+((5pi)/3)((sqrt(3))/2)+5/2`

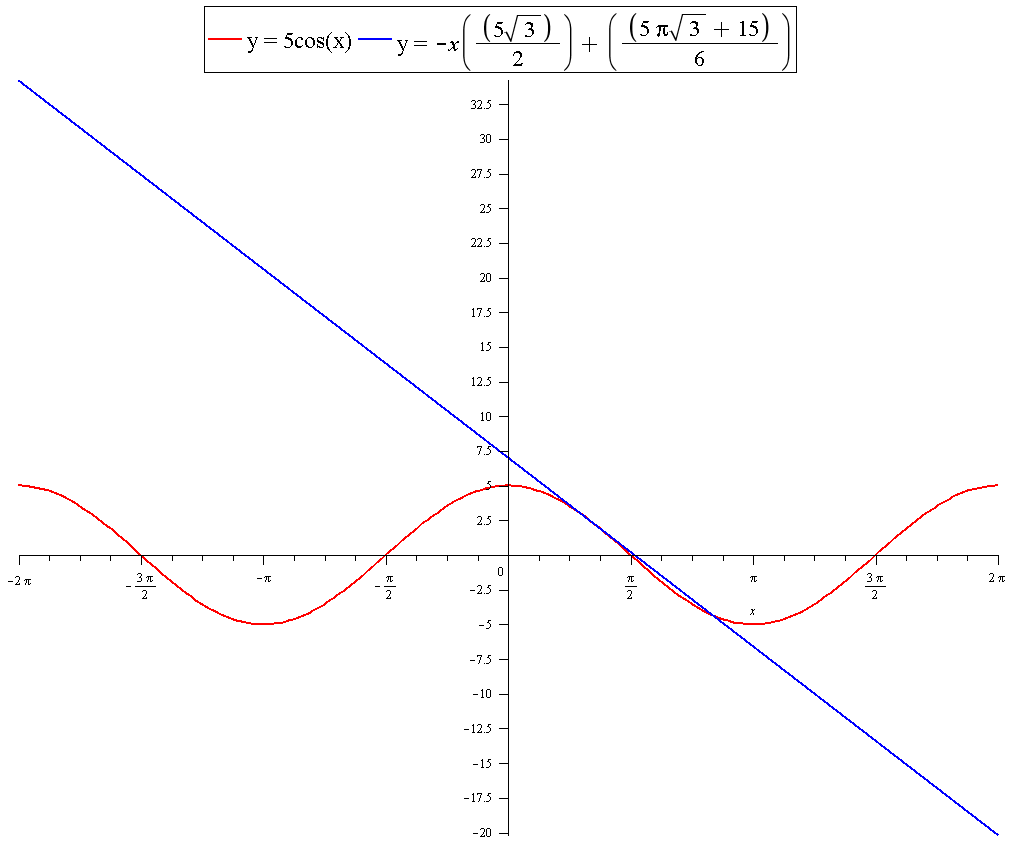
`color(blue)(y=-x((5sqrt(3))/2)+((5pisqrt(3)+15)/6))`

GRAPH: