Solve x^2-9 = tanx x2−9=tanx ?
1 Answer
Explanation:
There are a few ways that i can think of:
Graphically...
We notice that the solutions of this particular equation is where the functions
Were i am assuming you understand radians...
Hence graphing:
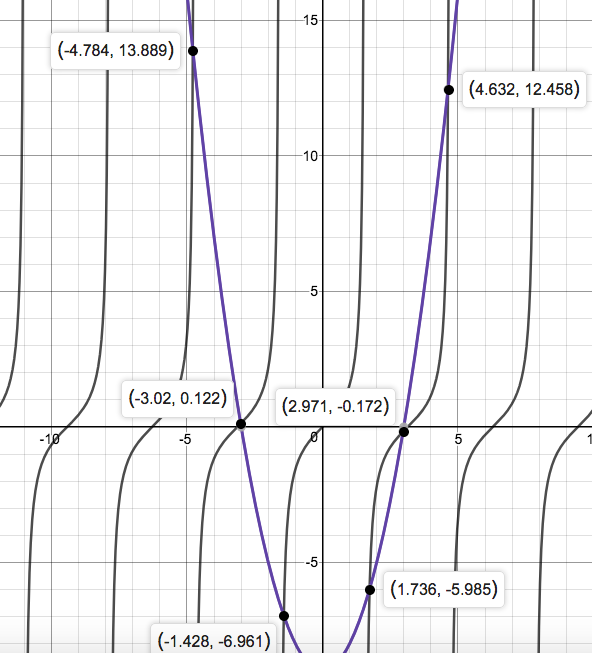
We can make out the approximate solitions for
The other way i can breifly describe is a method called Newton- Raphson...
Where you can solve
Where
So we can use this with
for more info about newton-raphson methods:

