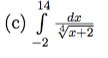First note that
int dx/(x+2)^(1/4)=int (x+2)^(-1/4)dx=4/3 (x+2)^(3/4)+C.
Next, note that the "impropriety" in the definite integral occurs at x=-2 because the function has a vertical asymptote there. Hence,
int_{-2}^{14}dx/(x+2)^(1/4)=lim_{a->-2+}int_{a}^{14}dx/(x+2)^(1/4)
assuming this limit exists, where the positive sign to the right of -2 in the limit indicates that a is approaching -2 from the right.
By the Fundamental Theorem of Calculus,
int_{a}^{14}dx/(x+2)^(1/4)=4/3 (x+2)^(3/4)|_{a}^{14}
=4/3 * 16^(3/4) - 4/3(a+2)^(3/4)=32/3 - 4/3(a+2)^(3/4).
Since lim_{a->-2+}(a+2)^(3/4)=0^(3/4)=0, it follows that the improper integral converges to 32/3.
We therefore write
int_{-2}^{14}dx/(x+2)^(1/4)=32/3.