Solve: 5sin theta = 6 cos^2theta -6 for theta in [0, 2pi]?
2 Answers
Explanation:
Hence,
We can see these results from the zeros of the graph of
graph{sinx(5+6sinx) [-1.56, 7.21, -1.892, 2.49]}
Explanation:
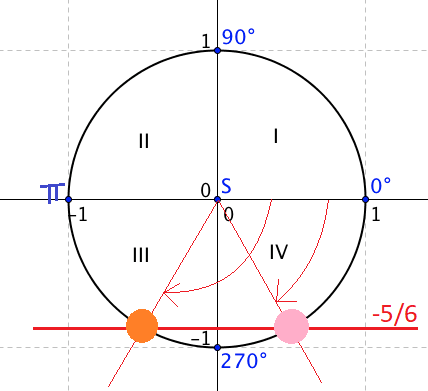
To find that you have to use calculator but it will tell you only one value. To find second value we need to know in which quadrant we are.
but
That means that the last angle must be in 3rd quadrant. To calculate that we use well known trick:
For 3rd quadrant:
Applying to our case: