How to do this?
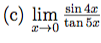
2 Answers
Explanation:
Quick method
Note that:
#lim_(t->0) sin t / t = 1#
#lim_(t->0) tan t / t = 1#
That is, both
So:
#lim_(x->0) (sin 4x) / (tan 5x) = lim_(x->0) (4x)/(5x) = 4/5#
L'Hôpital's rule method
Note that:
#lim_(x->0) sin 4x = 0#
#lim_(x->0) tan 5x = 0#
So the requested limit is an indeterminate form
#lim_(x->0) (sin 4x)/(tan 5x) = lim_(x->0) (d/(dx) sin 4x)/(d/(dx) tan 5x)#
#color(white)(lim_(x->0) (sin 4x)/(tan 5x)) = lim_(x->0) ((d/(dx) 4x)(cos 4x))/((d/(dx) 5x)(sec^2 5x))#
#color(white)(lim_(x->0) (sin 4x)/(tan 5x)) = lim_(x->0) (4 cos 4x)/(5 sec^2 5x)#
#color(white)(lim_(x->0) (sin 4x)/(tan 5x)) = (4 * 1)/(5 * 1)#
#color(white)(lim_(x->0) (sin 4x)/(tan 5x)) = 4/5#
Explanation:
Since
Now, arrange to
If the factors are canceled out, this will be equal to the previous expression. The reason for this arrangement is to exploit the identity
Then, we have
As
Now we can use
We can verify this limit with a graph:
graph{sin(4x)/tan(5x) [-1,1,-1,1]}
As seen, as


