Question

How do I prove these couple of sets? thanks

a) `A ⊂ B <=> A ∪ B = B`

b) `(A - B) ∪ (B - A) = (A ∪ B) - (A ∩ B)`

Answer 1

See below.

Explanation:

a.) `A sub B hArr A uu B = B`

Before a more formal proof, we can get an intuitive understanding about why this is true. `A sub B` means that the set A is a subset of the set B. This means that all elements of A must also be elements of B.

Here is a visualization:

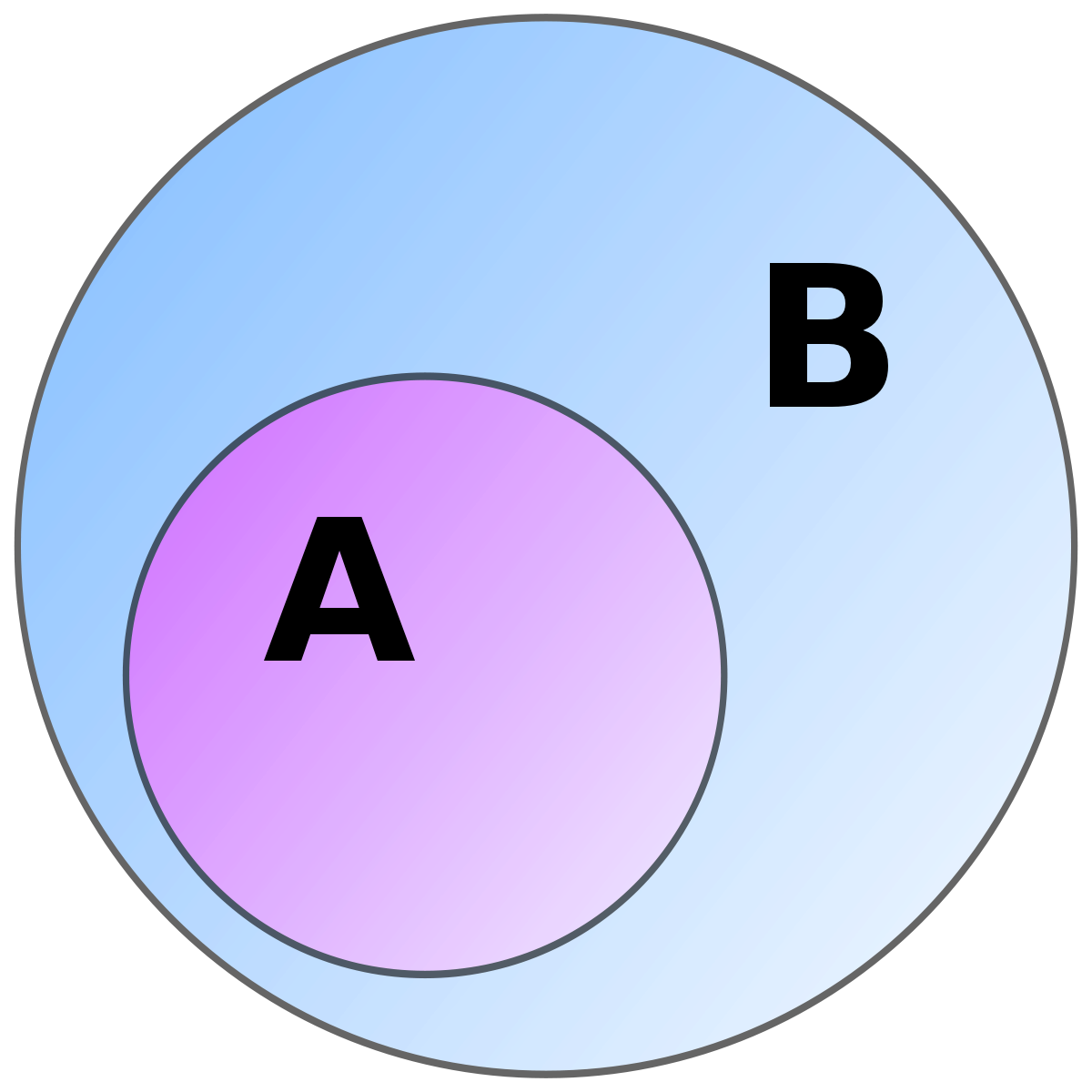
The next part (`A uu B = B`) tells us that if we combine the sets A and B, we get B. This fits with what we found above. Since A is completely contained within B (A is a subset of B), putting A and B together just gives us B.

The symbol between (`hArr`) tells us that the left side implies the right, and the right side implies the left. In other words, this is an if and only if (iff) statement. It reads "A is a subset of B if and only if `A uu B = B`."

Let's look at how to prove this. Since it is an iff statement, we will have to prove it both ways.

Proof.

Let A and B be sets with `A sub B`. Let `x in A`. Then, by definition of subset, `x in B` for all `x in A`. So, if `x in B`, then `x in A uu B`.

Now let `x in A uu B`. Then `x in A` or `x in B`. If `x in B`, then clearly this statement is true. If `x in A`, then it must be that `x in B`, since `A sub B`. In either case, `x in B`.

We have shown that if `A sub B` then `A uu B sub B` and `B sub A uu B`. Hence, `A uu B = B`.

Now assume `A uu B = B`. Let `x in A` be an arbitrary element. Since `x in A`, it follows that `x in A` or `x in B`. Equivalently, `x in A uu B`. But `A uu B= B`. Hence, `x in B`. `square`

b.) `(A-B)uu(B-A) = (AuuB)-(AnnB)`

Proof.

Let A and B be sets and let `x in ((A-B)uu(B-A))`. Then, by definition of union, `x in (A-B)` or `x in (B-A)`.

If `x in (A-B)`, then `x in A` and `x !in B`, by definition of complement. If `x in (B-A)`, then `x in B` and `x !in A`. Then it follows that `x in B` or `x in A`, or it must be that `x in A^c` or `x in B^c`. Equivalently, `x !in (AuuB)` or, `x in (A nn B)^c`. Hence, `x in ((AuuB)-(AnnB))` by definition of complement.

Now let `x in ((AuuB)-(AnnB))`. Then `x in (A uu B)` and `x in bar(AnnB)`, by definition of complement. Therefore `x in A` or `x in B`, and `x in (A-B)` or `x in (B-A)`. Equivalently (removing the redundancy), `x in ((A-B)uu(B-A))`.

`:. (A-B)uu(B-A) = (AuuB)-(AnnB) square`

Drawing venn diagrams is a great way to visualize these types of statements and to make sense of them as you go. If you're unsure of any of the above claims, try drawing a picture.