Question #05a9c

1 Answer
zhirou
Jan 8, 2018

#0.67# drops of water.

Explanation:

First, we need to find out how much the #4*10^23# molecules of water weighs. To do this, we can use this equation:

#"number of molecules in sample ⋅ mass of one molecule"#
#"= mass of sample"#

The mass of one water molecule is #"18.02 amu"#, because:

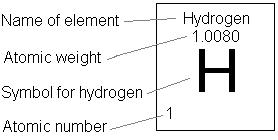
  1. We know water is #H_2O#.
  2. By looking at the periodic table, we can find the masses of hydrogen and oxygen—#"1.008 amu"# and #"16.00 amu"#, respectively.
    Water/Wastewater Distance Learning Website
    (The unit used is #"amu"# because the mass of one atom is too small to be dealt with in terms of grams.)
  3. #"mass of 2 hydrogen atoms + mass of 1 oxygen atom"#
    #"= mass of 1 water molecule"#
  4. #(2*"1.008 amu") + "16.00 amu" = "18.02 amu"#

The equation at the beginning can now be applied:

#"number of molecules ⋅ mass of one molecule = mass of sample"#

#(4*10^23) * "18.02 amu" = 7.208 * 10^24 "amu"#

As the mass of the drop of water was given in grams, #7.208 * 10^24 "amu"# also needs to be converted into grams.
#"1 amu"# = #1.66 * 10^-24"g"#, so:
#7.208 * 10^24 "amu" = "11.97g"#

Then, we just divide #"11.97g"# by #"18g"#, the mass of the drop of water, to find how many drops can fit into #"11.97g"#.

#("11.97g")/("18g")="0.67 drops"#

Related questions
Impact of this question
1279 views around the world
You can reuse this answer
Creative Commons License